Looking for practice Year 11 Chemistry questions?
We’ve compiled a comprehensive list of the most common questions which appear in Year 11 Chemistry yearly exams. These exam-style questions with detailed worked solutions provide full coverage over all four modules:
- Module 1: Properties and Structure of Matter
- Module 2: Introduction to Quantitative Chemistry
- Module 3: Reactive Chemistry
- Module 4: Drivers of Reactions
In this article, you’ll find Year 11 Chemistry questions on:
Year 11 Chemistry Questions on Module 1 ‘Properties and Structure of Matter Questions’
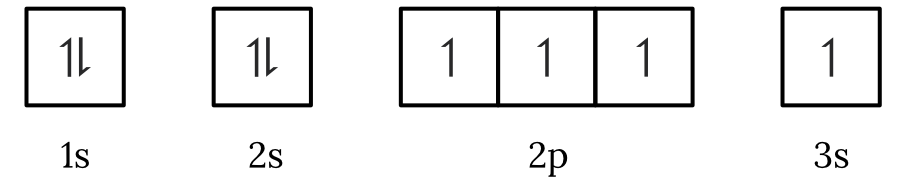
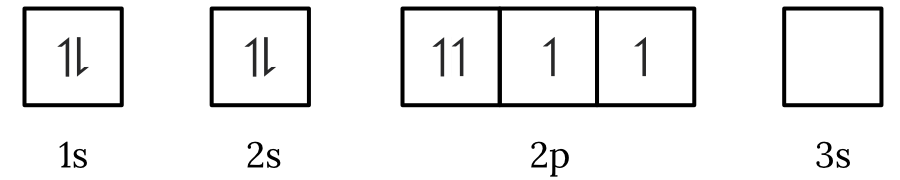
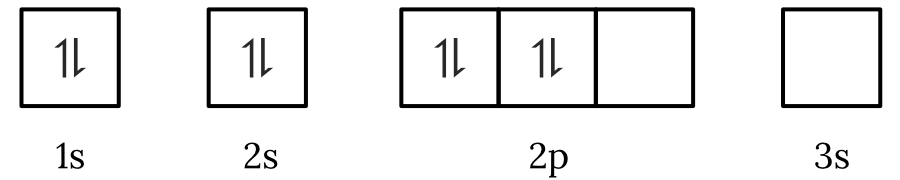
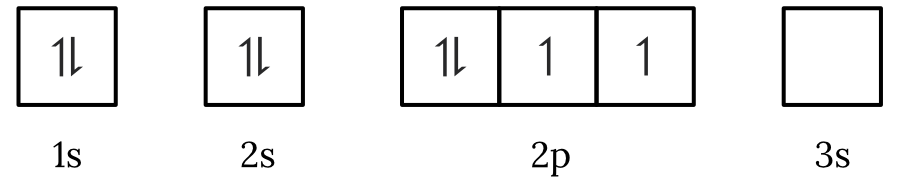
Question 1 – Electronic configuration
Which of the following electron spin-orbital diagrams do not obey the Aufbau principle?
See Question 1 Solution
Question 2 – Periodicity
Arrange the following elements \small X, Y and \small Z in order of increasing electronegativity.
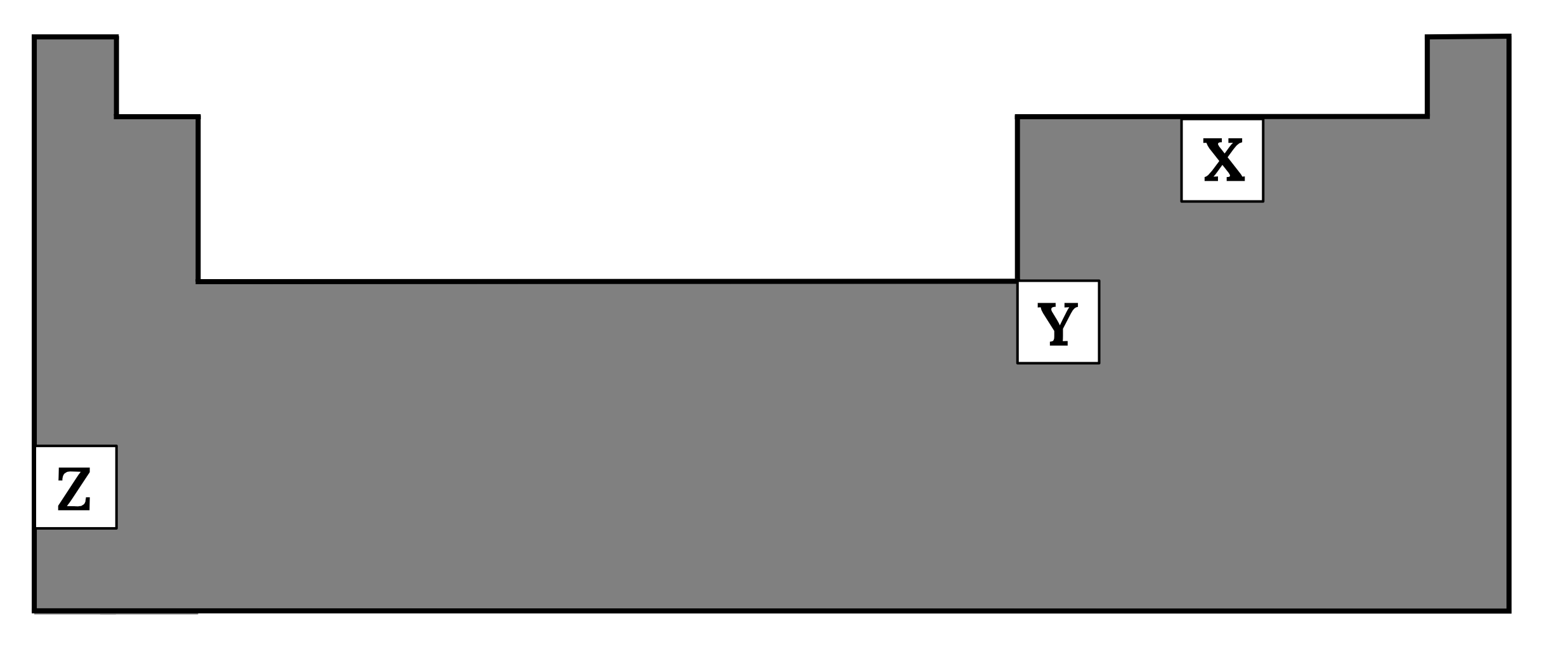
Justify your answer. (4 marks)
See Question 2 Solution
Question 3 – Lewis dot structure, molecular shape and polarity
Phosphorus trichloride has a boiling point of 76 \small \degree \text{C} .
Identify the dominant intermolecular forces which exist in phosphorus trichloride at room temperature. Justify your answer with reference to the molecular geometry of the compound. (2 marks)
See Question 3 Solution
Question 4 – Physical properties of substances
The table below shows the boiling and melting points of different substances.
| \small \boldsymbol{KBr} | \small \boldsymbol{SO_2} | \small \boldsymbol{SiO_2} |
| Boiling point ( \small \degree \text{C}) | 1435 | -10.3 | 2230 |
| Melting point ( \small \degree \text{C}) | 730 | -75.7 | 1710 |
Account for the differences between the boiling and melting points between the substances. (3 marks)
See Question 4 Solution
Question 5 – Nuclear chemistry
Consider the following nuclear reaction.
\large {{90 \atop 38} Sr \rarr X + {0 \atop -1}e}
What is the missing element X?
| (A) | {91 \atop 39}Zr |
| (B) | {91 \atop 38}Sr |
| (C) | {90 \atop 37}Rb |
| (D) | {90 \atop 39}Y |
See Question 5 Solution
Year 11 Chemistry Questions on Module 2 ‘Introduction to Quantitative Chemistry’
Question 6 – Mole calculation
How many chloride ions are there in 10 \small \text{mL} of 2.0 \small \text{M} hydrochloric acid? (2 marks)
See Question 6 Solution
Question 7 – Empirical formula calculation
A student performed a first-hand investigation to measure the mass of the elements in magnesium oxide by heating a piece of magnesium in a crucible.
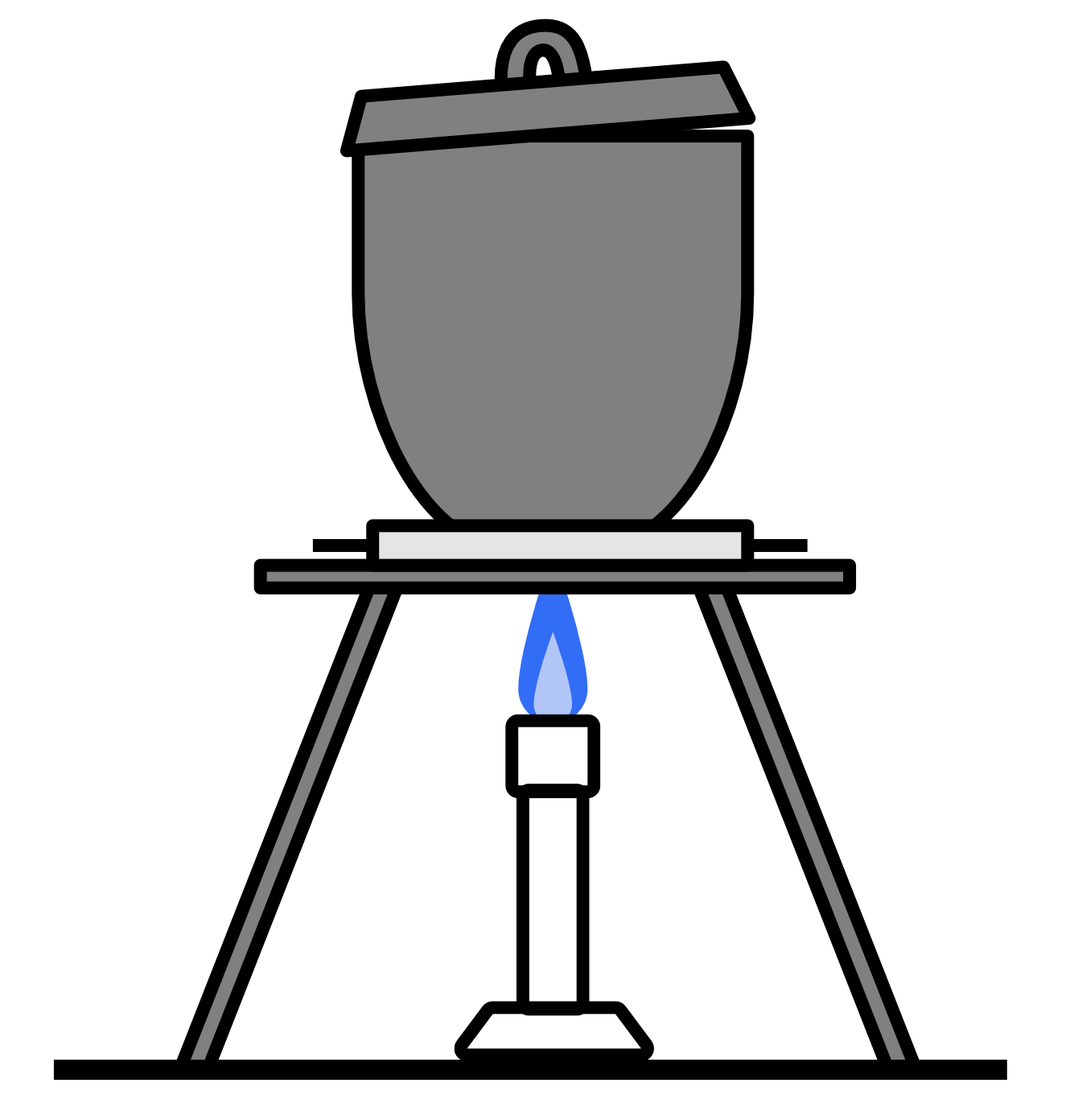
The magnesium reacts with oxygen in the air according to the following formula:
{Mg}_{(s)} + {O_2}_{(g)} \rarr {MgO}_{(s)}
The data from this investigation is recorded in the table below.
| Component | Mass \small (\textbf{g}) |
| Mass of dry crucible + lid | 29.80 |
| Mass of dry crucible + lid + magnesium | 30.34 |
| Mass of dry crucible + lid + magnesium oxide | 30.70 |
Determine the empirical formula of magnesium oxide. (3 marks)
See Question 7 Solution
Question 8 – Application of gas laws
When a balloon at room temperature of 25 \small \degree \text{C} is submerged in liquid nitrogen, the volume of the balloon decreases by 65%.
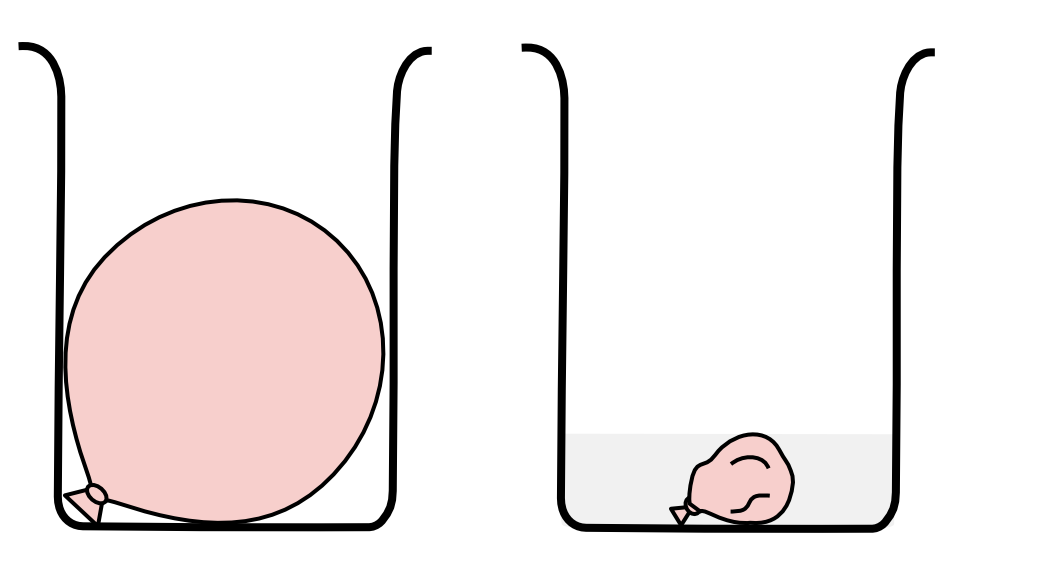
If the pressure remains constant and the temperature of the gases inside the balloon is 10 \small \degree \text{C} higher than the temperature of liquid nitrogen, calculate the temperature of liquid nitrogen. (4 marks)
See Question 8 Solution
Question 9 – Dilution calculations
7.6 \small \text{g} of sodium chloride is dissolved in water and made up to 250 \small \text{mL} in a volumetric flask. 10 \small \text{mL} of this solution was then diluted with 40 \small \text{mL} of distilled water.
| a) | Calculate the concentration of the concentrated solution. | 1 mark |
| b) | Calculate the concentration of the diluted solution. | 2 marks |
See Question 9 Solution
Question 10 – Limiting reagent calculation
2.5 \small \text{g} of barium chloride powder is added to 10 \small \text{mL} of 1.0 molar sodium sulfate solution.
| a) | Write a balanced chemical equation for this reaction. | 1 mark |
| b) | Identify the limiting reagent. | 2 marks |
| c) | Calculate the mass of precipitate formed. | 2 marks |
| d) | Calculate the mass of the remaining excess reagent. | 2 marks |
See Question 10 Solution
Year 11 Chemistry Questions on Module 3 ‘Reactive Chemistry’
Question 11 – Reactions of metals
During an experiment, metal A was placed in a beaker containing a solution of metal B2+ ions. After a while, a layer of deposit formed on metal A as shown in the diagram below.
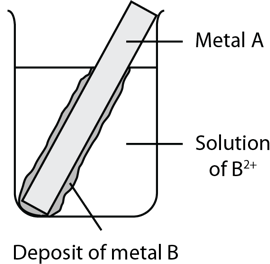
If metal A reacts slowly in concentrated acid, predict the behaviour of metal B in a 1.0 M solution of concentrated hydrochloric acid. (3 marks)
See Question 11 Solution
Question 12 – Oxidation numbers and net ionic equations
When aluminium metal is added to a solution of bright blue copper sulfate, a brown precipitate forms on the metal and the colour of the solution changes to clear and colourless.
| a) | Write a balanced full formula and net ionic equation for this reaction. | 2 marks |
| b) | Identify the change in the oxidation number of the aluminium. | 1 mark |
| c) | Hence or otherwise, determine the oxidising agent and the reducing agent, | 1 mark |
See Question 12 Solution
Question 13 – Galvanic cells and redox reactions
The following galvanic cell is constructed.
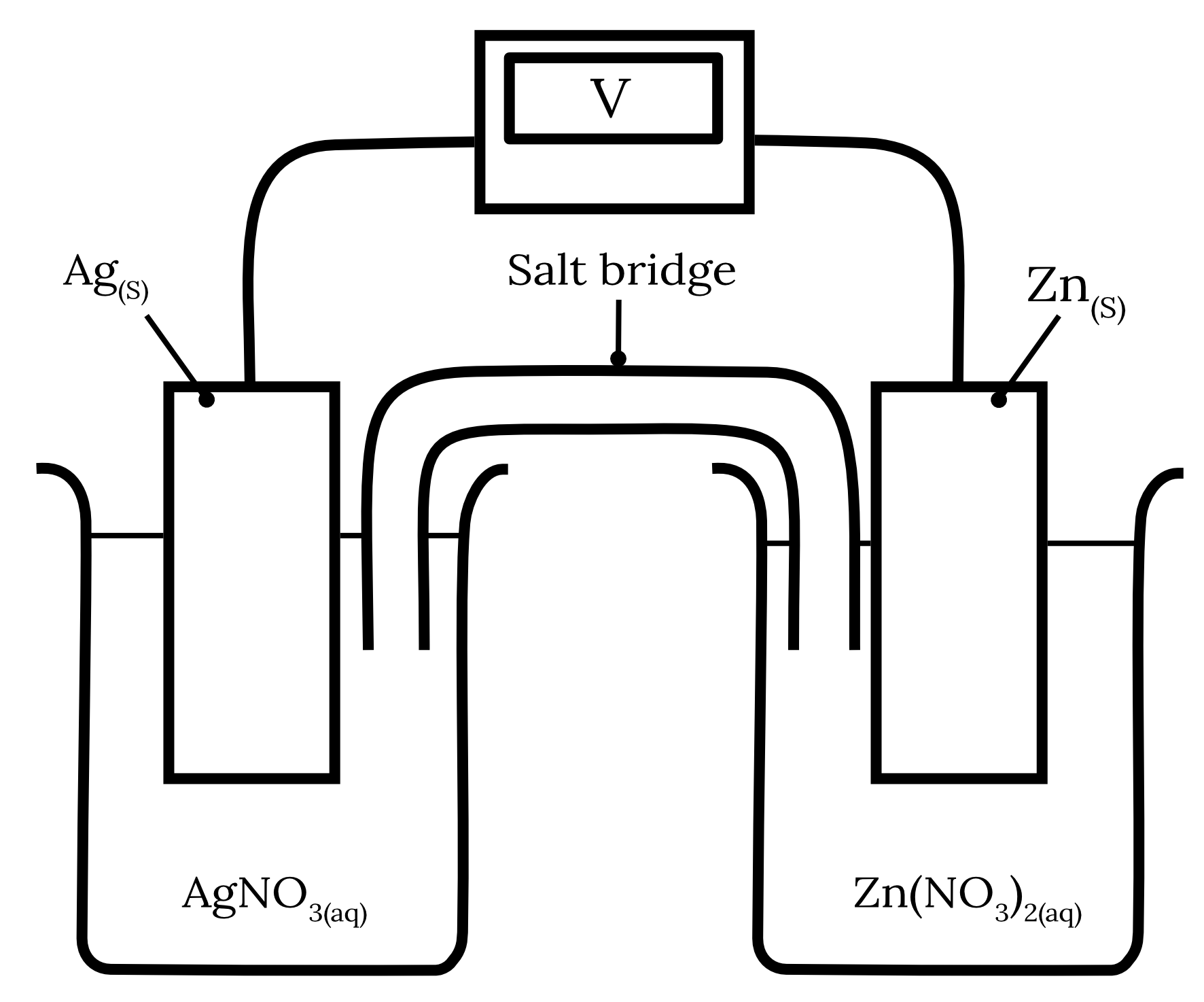
| a) | Write the half equations and the overall cell equation for this galvanic cell. | 3 marks |
| b) | Indicate the direction of electron flow. | 1 mark |
| c) | Explain why sodium chloride salt bridge would not be suitable for this galvanic cell and suggest more suitable alternatives. | 2 marks |
See Question 13 Solution
Question 14 – Cell potential calculations
Consider the following galvanic cell.
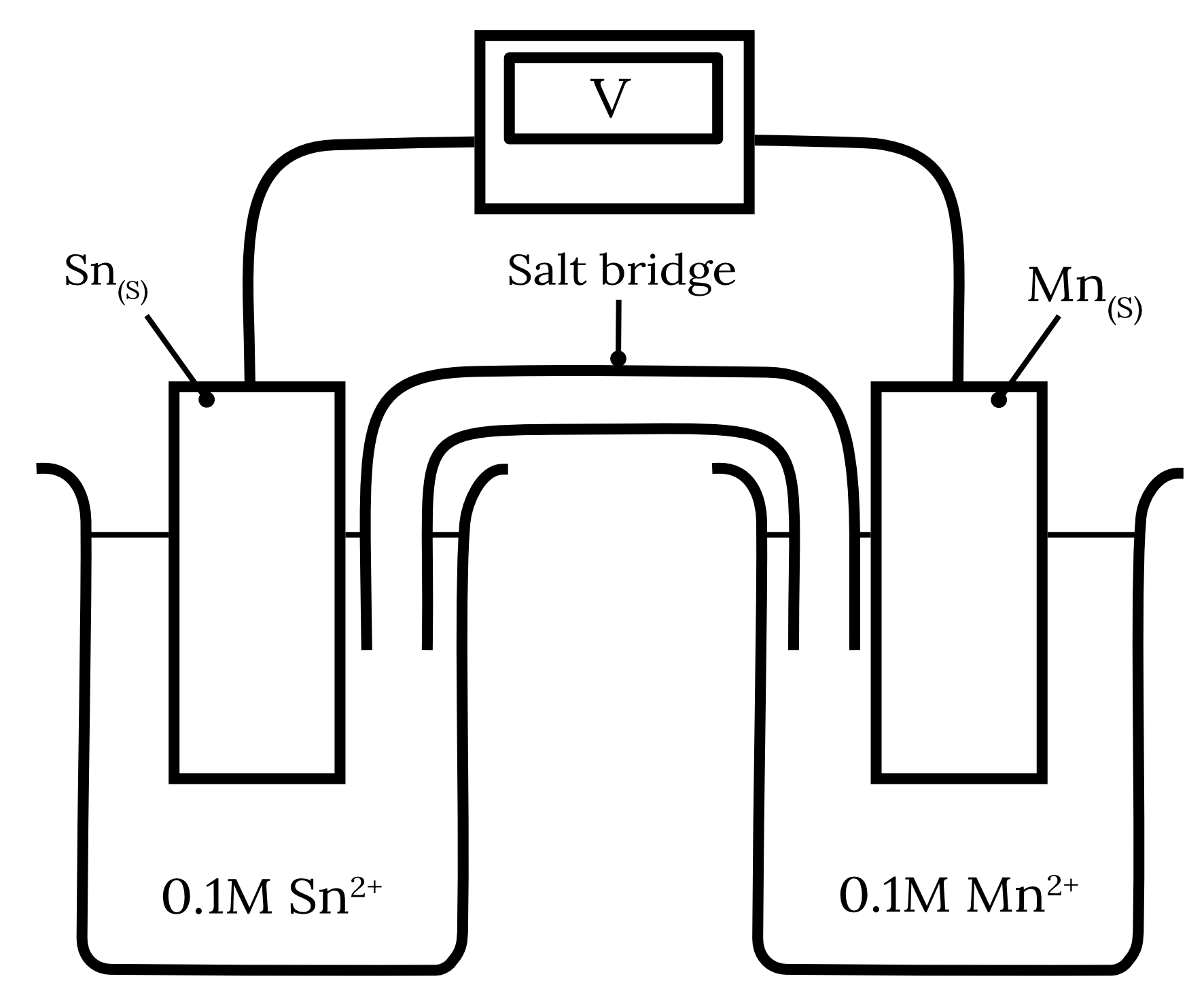
| a) | Calculate the standard cell potential for this galvanic cell. | 2 marks |
| b) | Over the course of the experiment, the cathode gained 0.64 \small \text{g} . If the starting mass of the anode was 4 \small \text{g} calculate the final mass of the anode. | 2 mark |
See Question 14 Solution
Question 15 – Rate of reaction
A group of students was trying to produce hydrogen gas by reacting metals with hydrochloric acid. They found that an iron nail reacted too slowly in 0.5 \small \text{M } HCl .
Suggest four ways they can modify their experiment to increase the rate of hydrogen production. (4 marks)
See Question 15 Solution
Want to practice more Year 11 Chemistry questions on Module 3 under exam conditions? Check out our Module 3 ‘Reactive Chemistry’ practice test!
Year 11 Chemistry Questions on Module 4 ‘Drivers of Reactions’
Question 16 – Calorimetry calculation
A calorimetry experiment was set up as follows.
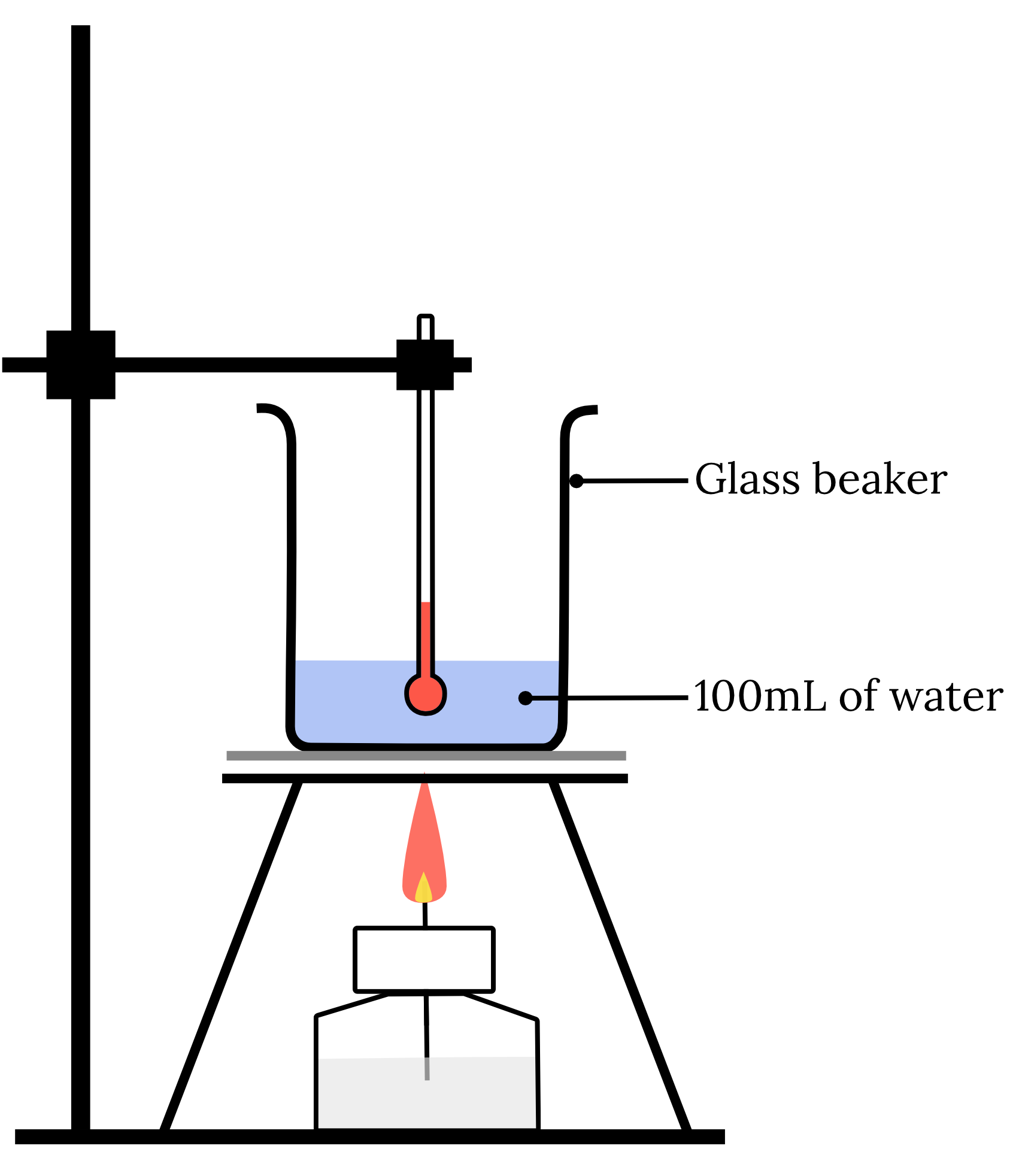
When 3.5 \small \text{g} of \small CH_3OH was burnt, the temperature of the water and the 25 \small \text{g} glass beaker was raised from 20.8 \small \degree \text{C} to 36.5 \small \degree \text{C} .
The specific heat capacity of glass is 0.840 x 103 \small \text{J kg}^{-1}\text{mol}^{-1}.
Assuming all of the energy produced in the combustion was used to heat the water and glass beaker, determine the enthalpy of combustion of \small CH_3OH .
See Question 16 Solution
Question 17 – Bond energies
Consider the following reaction.

Using the table of average bond energies below, calculate the change in enthalpy for this reaction.
| Bond | Average Energy \small (\textbf{kJ mol}^\bold{-1}) |
| C\equiv O | 1072 |
| C=O | 804 |
| O-H | 463 |
| H-H | 436 |
See Question 17 Solution
Question 18 – Hess’s law
Calculate the enthalpy of formation of gaseous formaldehyde \small (H_2CO) using the following information. (5 marks)
\begin{aligned} {H_2CO}_{(g)} \kern{1cm} \Delta H_c^\circ &= -563.5 \text{ kJ mol}^{-1} \\\\ {CO_2}_{(g)} \kern{1cm} \Delta H_f^\circ & = -393.5 \text{ kJ mol}^{-1} \\\\ {H_2O}_{(l)} \kern{1cm} \Delta H_f^\circ & = -285.8 \text{ kJ mol}^{-1} \end{aligned}
See Question 18 Solution
Question 19 – Predicting entropy changes
Predict the sign of the change in entropy for the following reaction. (2 marks)
2{HCl}_{(g)} + {C_2H_2}_{(g)} \rarr {C_2H_4Cl}_{(l)}
See Question 19 Solution
Question 20 – Gibbs free energy and spontaneity
The balanced chemical equation for the process of respiration is shown below.
{C_6H_{12}O_6}_{(s)} + {6O_2}_{(g)} \rarr 6{CO_2}_{(g)} + 6{H_2O}_{(l)}
Standard enthalpy of formation and standard entropy is given in the table below.
| Substance | \small \Delta \boldsymbol{H^{\circ}_f} \ \boldsymbol{(\bold{kJ \ mol}^{\bold{-1}})} | \small \boldsymbol{S^\bold{{\circ}}} \ \boldsymbol{(\bold{J \ K}^{\bold{-1}} \ \bold{mol}^{\bold{-1}})} |
| {C_6H_{12}O_6}_{(s)} | -1274 | 212.0 |
| {O_2}_{(g)} | 0 | 205.1 |
| {CO_2}_{(g)} | -393.5 | 213.7 |
| {H_2O}_{(l)} | -285.8 | 69.91 |
Determine the temperature ranges for which respiration is spontaneous. \small \text{K} .
See Question 20 Solution
Solutions to Year 11 Chemistry Questions
| Q | Answer |
| 1 | Answer (A) The Aufbau principle states that electrons fill the lowest available energy levels first. Since, the \small 2p orbitals have a lower energy than the \small 3s orbital, the electrons will fill the \small 2p first. Therefore, the electron spin-orbital diagram in option (A) violates the Aufbau principle. Back to question 1 |
| 2 | The elements are \small Z, Y, X in order of increasing electronegativity. This is due to the fact that electronegativity increases from left to right across a period and decreases down a group. Across a period, consecutive elements have one more proton but the same number of electron shells. Therefore, the nuclear charge increases but the effect of electron shielding is mostly unchanged. Hence the nucleus can exert a greater attraction to electrons. Thus, electronegativity increases across a period. Down a group, successive elements have a greater number of protons and electron shells. However, the effect of shielding increases more than the attraction from the increased nuclear charge. Hence the nucleus can exert a smaller attraction to electrons. Thus, electronegativity decreases down a group. Back to question 2 |
| 3 | As seen in the Lewis structure below, phosphorous trichloride \small PCl_3 has 4 VSEPR groups around the central phosphorous atom, one of which is a lone pair. Therefore, the molecule has a trigonal pyramidal geometry with the bond dipole moments pointing away from the central phosphorus atom. Thus, the net dipole moment is non-zero and the molecule is polar and experiences dipole-dipole forces as the dominant intermolecular force. 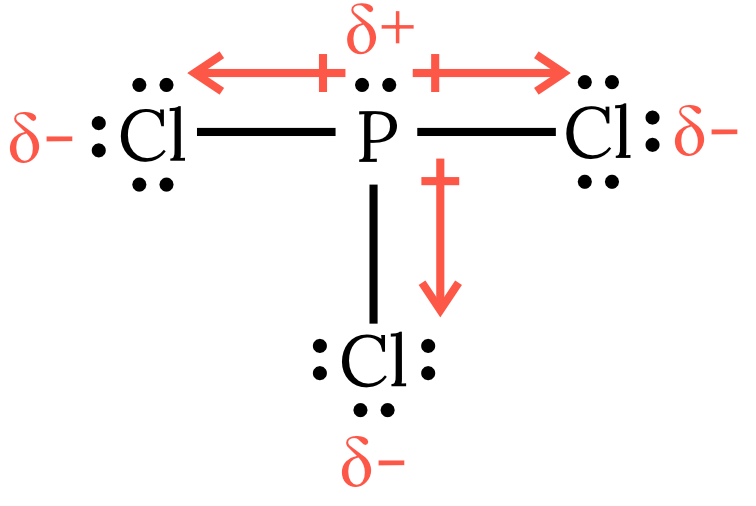
Back to question 3 |
| 4 | \small KBr is an ionic compound, held together by strong ionic bonds. \small SO_2 is a covalent molecular compound. The discrete \small SO_2 molecules are held together by relatively weak intermolecular forces. \small SiO_2 is a covalent network substance that is held together in a lattice by extremely strong covalent bonds. Covalent bonds in a lattice network are stronger than ionic bonds which are in turn stronger than intermolecular forces. Therefore, more thermal energy, and thus higher temperatures, are required to break the covalent bonds in \small SiO_2 than that which is required to break the ionic bonds in \small KBr and the weak intermolecular forces in \small SO_2 . As such, the boiling point (BP) and melting point (MP) of \small SiO_2 is much higher than the BP and MP of \small KBr which is again higher than the BP and MP of \small SO_2 . Back to question 4 |
| 5 | Answer (D) {90 \atop 38} Sr \rarr \boldsymbol{{90 \atop 39}Y} + {0 \atop -1}e Back to question 5 |
| 6 | Step 1: Write a balanced equation. {HCl}_{(aq)} \rarr {H^+}_{(aq)} + {Cl^-}_{(aq)} Step 2: Calculate the moles of the known substance from the known quantity. \begin{aligned} n(HCl) & = c \times V \\ \\ & = 2.0 \times 0.010 \\ \\ & = 0.020 \text{ mol} \end{aligned} Step 3: Calculate the moles of the unknown substance using mole ratios. \begin{aligned} n(Cl^-) &= n(HCl) \\\\ &=0.020 \text{ mol} \end{aligned} Step 4: Convert the moles to the desired quantity. \begin{aligned} \text{number of } Cl^- \text{ ions } & = n \times N_A \\ \\ & = 0.020 \times 6.022 \times 10^{23} \\ \\ & = 1.2 \times 10^{22} \text{ (2 s.f.)} \end{aligned} Back to question 6 |
| 7 | Step 1: Calculate the mass of \small Mg. \begin{aligned} m(Mg) &= 30.34 - 29.80 \\ \\ &= 0.54 \text{ g} \end{aligned} Step 2: Calculate the moles of \small Mg. \begin{aligned} n(Mg) &= \dfrac{0.54}{24.31} \\ \\ &= 0.0222 \text{ mol} \end{aligned} Step 3: Calculate the mass of \small O. \begin{aligned} m(O) &= 30.70-30.34 \\ \\ & = 0.35\ \text{ g} \end{aligned} Step 4: Calculate the moles of \small O. \begin{aligned} n(O) &= \dfrac{0.35}{16.00} \\ \\ &= 0.0225 \text{ mol} \end{aligned} Step 5: Convert the mole ratio to the simplest whole number ratio \begin{aligned} n(Mg) : n(O) &= 0.0222:0.0225 \\ & \approx 1:1 \end{aligned} Therefore, the empirical formula is \small MgO. Back to question 7 |
| 8 | Step 1: Identify the known quantity and the desired quantity. \begin{aligned} T_1 &= 25 \degree \text{C} \\\\ T_2 & = \ ? \\\\ V_2 & = (1-0.65) \times V_1 \\\\ & = 0.35 \times V_1 \end{aligned} Step 2: Write the formula that relates the known and desired quantities. \dfrac{V_1}{T_1} = \dfrac{V_2}{T_2} Step 3: Calculate the desired quantity. \begin{aligned} \frac{V_1}{T_1} &= \frac{V_2}{T_2} \\\\ \frac{\cancel{V_1}}{25+273.15} & = \frac{0.35 \times \cancel{V_1}}{T_2} \\\\ \frac{1}{25+273.15}&=\frac{0.35}{T_2} \\\\ T_2 &= 0.35 \times (25+273.15) \\\\ & = 104.35 \text{ K} \\\\ \therefore T_2 & = -168.80 \degree \text{C} \end{aligned} The temperature of the gases inside the balloon is 10 \small \degree \text{C} higher than the temperature of liquid nitrogen. \begin{aligned} T_\text{ liquid nitrogen} & = -168.8 -10 \\\\ & = -178.8 \degree \text{C} \end{aligned} Therefore, the temperature of liquid nitrogen is -178.8 \small \degree \text{C} . Back to question 8 |
| 9 | Part a) \begin{aligned} n(NaCl) & = \frac{m}{MM} \\\\ & = \frac{7.6}{(22.99 + 35.45)} \\\\ & = 0.13 \\\\ [NaCl] &= \frac{n}{V} \\\\ & = \frac{0.13}{0.250} \\\\ \therefore [NaCl] & = 0.52 \text{ mol L}^{-1} \text{(2 s.f.)} \end{aligned} Part b) Step 1: Identify the known and the desired quantity. c_1 = 0.52 \text{ mol L}^{-1} V_1 = 10 \text{ mL} V_2 = 10+40 = 50 \text{ mL} Step 2: Write the formula that relates the known and desired quantities. c_1V_1 = c_2V_2 Step 3: Calculate the desired quantity. \begin{aligned} c_1V_1 & = c_2V_2 \\\\ c_2 & = \frac{c_1V_1}{V_2} \\\\ & = \frac{0.52 \times 10}{50} \\\\ & = 0.10 \text{ mol L}^{-1} \text{(2 s.f.)} \end{aligned} Back to question 9 |
| 10 | Part a) {BaCl_2}_{(s)} + {Na_2SO_4}_{(aq)} \rarr {BaSO_4}_{(s)} + 2{NaCl}_{(aq)} Part b) Step 1: Calculate the moles of each reactant present. \begin{aligned} n(BaCl_2) & = \frac{m}{MM} \\\\ & = \frac{2.5}{(137.3 + 2\times 35.45)} \\\\ & =0.0120 \text{ mol} \\\\ n(Na_2SO_4) & = c\times V \\\\ & = 1.0 \times 0.010 \\\\ & = 0.010 \text{ mol} \end{aligned} Step 2: Determine the moles of a product formed from each reactant. \begin{aligned} 0.0120 \text{ mol}\ BaCl_2 &\rarr 0.0120 \text{ mol}\ BaSO_4\ (1:1\ \text{mole ratio}) \\\\ 0.010 \text{ mol}\ Na_2SO_4 &\rarr 0.010 \text{ mol}\ BaSO_4\ (1:1\ \text{mole ratio}) \end{aligned} Step 3: Identify the limiting reactant. From the calculations, \small Na_2SO_4 produces the least \small BaSO_4 . Therefore, \small Na_2SO_4 is the limiting reagent. Part c) \begin{aligned} n(BaSO_4) &= n(Na_2SO_4) \\\\ & = 0.010 \text{ mol} \\\\ m(BaSO_4) & = n \times MM \\\\ & = 0.010 \times (137.3 + 32.07 + 4 \times 16.00) \\\\ & = 2.3 \text{ g} \text{ (2 s.f.)} \end{aligned} Part d) \begin{aligned} n(BaCl_2)_\text{remaining} & = n(BaCl_2)_\text{initial} - n(BaCl_2)_\text{reacted} \\\\ & = 0.0120 - 0.010 \\\\ & = 0.0020 \text{ mol} \\\\ m(BaCl_2)_\text{remaining} & = n \times MM \\\\ & = 0.0020 \times (137.3 + 2\times 35.45) \\\\ & = 0.418 \\\\ \therefore m(BaCl_2)_\text{remaining} & = 0.42 \text{ g} \text{ (2 s.f.)} \end{aligned} Back to question 10 |
| 11 | The formation of the metal B deposit indicates that metal A has displaced metal B in the solution. Therefore metal A is the more active metal. If metal A only reacts slowly in concentrated acid, metal B would either react even more slowly in concentrated acid or not react at all. Back to question 11 |
| 12 | Part a)
Full formula equation: 2{Al}_{(s)} + 3{CuSO_4}_{(aq)} \rarr {Al_2(SO_4)_3}_{(aq)} + 3{Cu}_{(s)} Full ionic equation: 2{Al}_{(s)} + 3{Cu^{2+}}_{(aq)} + 3{{SO_4}^{2-}}_{(aq)} \rarr 2{Al^{3+}}_{(aq)} + 3{{SO_4}^{2-}}_{(aq)} + 3{Cu}_{(s)} Net ionic equation: 2{Al}_{(s)} + 3{Cu^{2+}}_{(aq)} \rarr 2{Al^{3+}}_{(aq)} + 3{Cu}_{(s)} Part b) The oxidation numbers of reach of the elements are shown below. 2\overset{\textcolor{ff5748}{0}}{{Al}}_{(s)} + 3\overset{\textcolor{326df5}{+2}}{{Cu}^{2+}}_{(aq)} \rarr 2\overset{\textcolor{ff5748}{+3}}{{Al^{3+}}}_{(aq)} + 3\overset{\textcolor{326df5}{0}}{{Cu}}_{(s)} Therefore the change in the oxidation number aluminium is +3. Part c) The oxidation number of aluminium has increased, while the oxidation number of copper has decreased. Therefore, aluminium has been oxidised, acting as the reducing agent while copper has been reduced, acting as the oxidising agent. Back to question 12 |
| 13 | Part a) Using the standard reduction potentials from HSC Data Sheet for zinc and silver, we can determine the following two redox half-equations and their corresponding standard potentials as shown in the table below. | Reactant | Half-equation | Standard potential \small \boldsymbol{(V)} | | Zinc | Zn^{2+} + 2e^- \rarr {Zn}_{(s)} | -0.76 | | Silver | Ag^+ + e^- \rarr {Ag}_{(s)} | 0.80 |
The standard reduction potential of zinc is more negative than silver. Therefore, zinc will undergo oxidation at the anode while silver will undergo reduction at the cathode. \begin{aligned} {Zn}_{(s)} &\rarr Zn^{2+} + 2e^- \kern{1cm} \text{ (oxidation)}\\\\ Ag^+ + e^- &\rarr {Ag}_{(s)} \kern{2.1cm} \text{ (reduction)} \\\\ 2{Ag}^+ + {Zn}_{(s)} &\rarr 2{Ag}_{(s)} + {Zn}^{2+} \kern{0.7cm} \text{ (overall equation)} \end{aligned} Part b) The electrons flow from the zinc anode to the silver cathode. 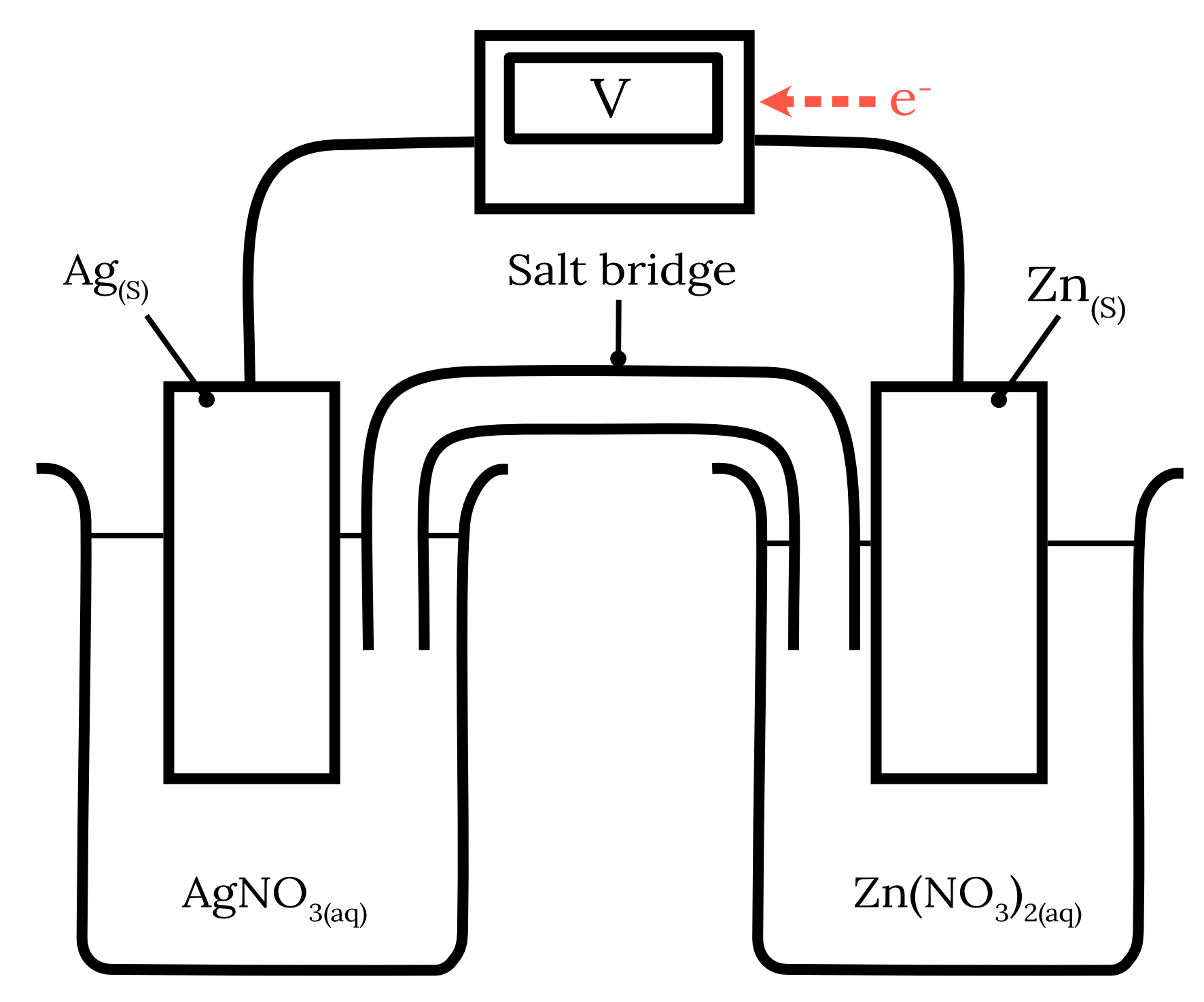
Part c) A sodium chloride salt bridge is not a suitable salt bridge for this galvanic cell as the chloride ions can form insoluble precipitates with the silver ions in the solution. {Ag^+}_{(aq)} + {Cl^-}_{(aq)} \rarr {AgCl}_{(s)} An example of a more suitable alternative is sodium nitrate. Back to question 13 |
| 14 | Part a) Step 1: Identify the half-equations from the table of standard reduction potentials. | Reactant | Half-equation | Standard potential \small \boldsymbol{(V)} | | Tin | {Sn}^{2+} + 2e^- \rarr {Sn}_{(s)} | -0.14 | | Manganese | {Mn}^{2+} + 2e^- \rarr {Mn}_{(s)} | -1.18 |
Step 2: Determine the standard potentials of the anode and cathode. The standard reduction potential of manganese is more negative than tin. Therefore, manganese will undergo oxidation at the anode while tin will undergo reduction at the cathode. \begin{aligned} {Mn}_{(s)} \rarr {Mn}^{2+} + 2e^- \kern{1cm} E_\text{\textcolor{326df5}{ox}}^\circ &= 1.18 \\\\ {Sn}^{2+} + 2e^- \rarr {Sn}_{(s)} \kern{1cm} E_\text{\textcolor{ff5748}{red}}^\circ &= -0.14 \end{aligned} Step 3: Calculate the standard cell potential of the electrochemical cell. \begin{aligned} E_\text{cell}^\circ & = E_\text{\textcolor{326df5}{ox}}^\circ + E_\text{\textcolor{ff5748}{red}}^\circ \\\\ & = (1.18) + (-0.14) \\\\ & = 1.04 \\\\ \therefore E_\text{cell}^\circ &= 1.04 \text{ V} \end{aligned} Part b) Step 1: Write a balanced overall cell equation for the galvanic cell. {Mn}_{(s)} + {Sn^{2+}}_{(aq)} \rarr {Mn^{2+}}_{(aq)} + {Sn}_{(s)} Step 2: Calculate the moles of the known substance from the known quantity. The question states that cathode gained 0.64 \small \text{g} . In part a) we found that tin was reduced and therefore is the cathode. \begin{aligned} m(Sn) &= 0.64 \text{ g} \\\\ n(Sn) & = \frac{m}{MM} \\\\ \frac{0.64}{118.7} \\\\ & = 0.00539 \dots \text{mol} \end{aligned} Step 3: Calculate the moles of the unknown substance using mole ratios. \begin{aligned} n(Mn) & = n(Sn) \\\\ & = 0.00539 \dots \text{mol} \end{aligned} Step 4: Convert the moles to the desired quantity. \begin{aligned} m(Mn)_\text{reacted} & = n\times MM \\\\ & = 0.00539 \dots \times 54.94 \\\\ & = 0.2962 \text{ g} \\\\ m(\text{Anode}) &= m(Mn)_\text{inital} - m(Mn)_\text{reacted} \\\\ & = 4 - 0.2962 \\\\ & = 3.7038 \\\\ \therefore m(\text{Anode})& = 3.7 \text{ g (2 s.f.)} \end{aligned} Back to question 14 |
| 15 | Possible answers include:- Increasing concentration of acid used. For example, use a 2.0 \small \text{M} solution of \small HCl.
- Using a more reactive metal such as magnesium.
- Using smaller pieces of metal to increase the surface area exposed to the acid.
- Conducting the experiment at a higher temperature, for example, by placing the reaction vessel in a warm water bath.
Back to question 15 |
| 16 | Step 1: Write a balanced chemical equation of the process. {CH_3OH}_{(l)} + \frac{3}{2} {O_2}_{(g)} \rarr 2{H_2O}_{(l)} + {CO_2}_{(g)} Step 2: Calculate the heat lost or gained by the substance (water and glass beaker). \small \begin{aligned} q_\text{ total} & = m_\text{ water }c_\text{ water }\Delta T + m_\text{ glass beaker } c_\text{ glass beaker }\Delta T \\ \\ & = 0.100 \times 4.18 \times 10^{3} \times (36.5-20.8) + 0.025 \times 0.840\times 10^{-3} \times (36.5-20.8) \\ \\ &= 6892.3 \text{ J} \end{aligned} Step 3: Calculate the heat lost or gained by the combustion process. \begin{aligned} q_\text{ combustion process} &= -q_\text{ substance} \\ \\ &=-6892.3 \text{ J} \\ \\ &=-6.8923 \text{ kJ} \end{aligned} Step 4: Calculate the enthalpy change of the process. \begin{aligned} n(CH_3OH) & = \dfrac{n}{MM} \\ \\ &=\dfrac{0.35}{12.01+4\times 1.008+16} \\ \\ &=0.0109 \dots \text{ mol} \end{aligned} \begin{aligned} \Delta H_c&=\dfrac{q_\text{ combustion process}}{n_\text{ combustion process}} \\ \\ & = -\dfrac{6.8923}{0.0109 \dots} \\ \\ \therefore \Delta H_c & = - 631 \text{ kJ mol}^{-1} \text{(3 s.f.)} \end{aligned} Back to question 16 |
| 17 | Step 1: Count the bonds present in the reactants and products. 
| Bond | Reactants | Products | | C \equiv O | 1 | 0 | | O-H | 2 | 0 | | C=O | 0 | 2 | | H-H | 0 | 1 |
Step 2: Calculate the enthalpy of reaction using the sum of the bond energies. {\Delta H}_{r} = \sum {{\Delta H}_{\text{ reactant bond energies}}} − \sum {{\Delta H}_{\text{ product bond energies}}} \begin{aligned} \sum {{\Delta H}_{\text{ reactant bond energies}}} &= (C\equiv O) + (2\times O-H) \\\\ & = (1072) + (2\times 463) \\\\ & = 1998 \text{ kJ mol}^{-1} \\\\ \sum{{\Delta H}_{\text{ product bond energies}}} & = (2 \times C=O) + (H-H) \\\\ & = (2\times 804 + 436) \\\\ & = 2044 \text{ kJ mol}^{-1}\end{aligned} \begin{aligned} {\Delta H}_{r} &= \sum {{\Delta H}_{\text{ reactant bond energies}}} − \sum {{\Delta H}_{\text{ product bond energies}}} \\\\ & = 1998 - 2044 \\\\ & = -46 \text{ kJ mol}^{-1} \end{aligned} Therefore, the change in enthalpy for this reaction is -46 \small \text{ kJ mol}^{-1} . Back to question 17 |
| 18 | Step 1: Write a balanced chemical equation of the desired process. {H_2}_{(g)} + C_{(s)} + \frac{1}{2}{O_2}_{g} \rarr {H_2CO}_{(g)} \kern{1cm} \Delta H_f^\circ (H_2CO) Step 2: Write the intermediate equations that can be used to represent the desired process. \begin{aligned} {H_2CO}_{(g)} + {O_2}_{(g)} \rarr {CO_2} + {H_2O}_{(l)} \kern{1cm} \Delta H_1 &= -563.5 \text{kJ mol}^{-1} \\\\ {C}_{(s)} + {O_2}_{(g)} \rarr {CO_2}_{(g)} \kern{1cm} \Delta H_2& = -393.5 \text{kJ mol}^{-1} \\\\ {H_2}_{(g)} + \frac{1}{2}{O_2}_{(g)} \rarr {H_2O}_{(l)} \kern{1cm} \Delta H_3 & = -285.8 \text{kJ mol}^{-1} \end{aligned} Step 3: Identify the reactants and products that only appear in one intermediate equation. \begin{aligned} \textcolor{326df5}{{H_2CO}_{(g)}} + {O_2}_{(g)} \rarr {CO_2}_{(g)} + {H_2O}_{(l)} \kern{1cm} \Delta H_1 &= -563.5 \text{kJ mol}^{-1} \\\\ \textcolor{7d5ee4}{{C}_{(s)}} + {O_2}_{(g)} \rarr {CO_2}_{(g)} \kern{1cm} \Delta H_2& = -393.5 \text{kJ mol}^{-1} \\\\ \textcolor{ff5748}{{H_2}_{(g)}} + \small{\frac{1}{2}}{O_2}_{(g)} \rarr {H_2O}_{(l)} \kern{1cm} \Delta H_3 &= -285.8 \text{kJ mol}^{-1} \end{aligned} Step 4: Adjust each intermediate equation and the corresponding enthalpy values if required. In the desired equation, formaldehyde is on the products side. {H_2O}_{(l)} + {CO_2}_{(g)} \rarr {O_2}_{(g)} + \textcolor{326df5}{{H_2CO}_{(g)}} \kern{1cm} \Delta H_1 = \textcolor{326df5}{-}(-563.5) \text{kJ mol}^{-1} The other two equations do not need to be adjusted. Step 5: Add the adjusted intermediate equations and the corresponding enthalpy values. \begin{array}{ccc} {H_2O}_{(l)} + {CO_2}_{(g)} \rarr {O_2}_{(g)} + {{H_2CO}_{(g)}} &\Delta H_1 = +563.5 \text{kJ mol}^{-1} \\\\ {{C}_{(s)}} + {O_2}_{(g)} \rarr {CO_2}_{(g)} &\Delta H_2 = -393.5 \text{kJ mol}^{-1} \\\\ {{H_2}_{(g)}} + \small{\frac{1}{2}}{O_2}_{(g)} \rarr {H_2O}_{(l)} &\Delta H_3 = -285.8 \text{kJ mol}^{-1} \\\\ \hline \\ {H_2}_{(g)} + C_{(s)} + \frac{1}{2}{O_2}_{g} \rarr {H_2CO}_{(g)} &\Delta H_f^\circ = -115.8 \text{kJ mol}^{-1} \end{array} Therefore, the enthalpy of formation of formaldehyde is -115.8 \small \text{kJ mol}^{-1} \text{ (4 s.f.)} Back to question 18 |
| 19 | The number of moles of gas decreases as the reaction proceeds. Since gases have significantly higher entropy than liquids, the entropy of the reaction will decrease. The sign of \small \Delta S is negative. Back to question 19 |
| 20 | Step 1: Write a balanced chemical equation. {C_6H_{12}O_6}_{(s)} + {6O_2}_{(g)} \rarr 6{CO_2}_{(g)} + 6{H_2O}_{(l)} Step 2: Calculate the enthalpy and entropy changes of the system. Enthalpy: \begin{aligned} \Delta H_{r}^{\circ} &= \sum\Delta H^{\circ} _{f\text{ products}} − \sum\Delta H^{\circ}_{f\text{ reactants}} \\ \\ &= (6\times \Delta H^{\circ} _{f (CO_2)} + 6\times\Delta H^{\circ}_{f(H_2O)}) - ( \Delta H^{\circ}_{f(C_6H_{12}O_6)} + 6 \times \Delta H^{\circ}_{f(O_2)})\\ \\ &= (6 \times - 393.5 + 6 \times - 285.8) - (-1274 + 6 \times 0) \\ \\ &= -4075.8 + 1274 \\ \\ \therefore \Delta H_{r}^{\circ} &= -2801.8 \text{ kJ mol}^{-1} \\\\ \end{aligned} Entropy: \begin{aligned} \Delta S_{r}^{\circ} &= \sum S^{\circ} _{\text{ products}} − \sum S^{\circ}_{\text{ reactants}} \\ \\ &= (6 \times S^{\circ}_{CO_2} + 6\times S^{\circ}_{H_2O}) − (S^{\circ}_{C_6H_{12}O_6} + 6\times S^{\circ}_{O_2}) \\ \\ & = (6 \times 213.7 + 6 \times 69.91) - (212.0 + 6 \times 205.1) \\ \\ &= 1701.66 - 1442.6 \\ \\ &= 259.06 \text{ J K}^{-1} \text{ mol}^{-1} \end{aligned} Step 3: Convert the units of temperature, enthalpy and entropy changes if required. \begin{aligned} \Delta S & = 259.06 \text{ J K}^{-1} \text{ mol}^{-1} \\\\ & = 0.25906 \text{ kJ K}^{-1}\text{mol}^{-1} \end{aligned} Step 4: Substitute the terms into the equation for Gibbs free energy. \begin{aligned} \Delta G_r^\circ & = \Delta H_r^\circ - T \Delta S_r^\circ \\\\ \Delta G_r^\circ & = -2801.8 \text{ kJ mol}^{-1} - T\times 0.25906 \text{ kJ K}^{-1}\text{mol}^{-1} \end{aligned} Step 5: Calculate the temperature range for the reaction by setting Gibbs free energy to less than zero. \small \begin{aligned} \Delta G_r^\circ & = -2801.8 \text{ kJ mol}^{-1} - T\times 0.25906 \text{ kJ K}^{-1}\text{mol}^{-1} < 0 \\\\ 0&> -2801.8 \text{ kJ mol}^{-1} - T\times 0.25906 \text{ kJ K}^{-1}\text{mol}^{-1} \\\\ T\times 0.25906 \text{ kJ K}^{-1}\text{mol}^{-1} &> -2801.8 \text{ kJ mol}^{-1} \\\\ T & > \frac{-2801.8 \text{ kJ mol}^{-1}}{0.25906 \text{ kJ K}^{-1}\text{mol}^{-1}} \\\\ & > -10815 \text{ K} \end{aligned} Since the minimum possible temperature is absolute zero, (0 \small \text{ K} ). The reaction must be spontaneous for all temperatures. Back to question 20 |
Access over 1000+ Year 11 Chemistry Questions on Learnable
Test your understanding of any Year 11 Chemistry concepts with Learnable’s customisable quizzes. Try Learnable for free now.
Written by Varisara Laosuksri
Varisara is a 2019 St George Girls High School graduate who achieved Band 6 in her HSC Chemistry and Physics.
Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.