Physics Depth Study | The Comprehensive Guide
Looking for Physics depth study ideas and examples?
When you are given a Physics depth study assessment, you might be confused about where to start just like many students out there. In this article, we explain what depth studies are and the process of choosing your depth study idea and topic.
This comprehensive guide to Physic Depth Study consists of the following chapters:
- Chapter 1: Depth study ideas and topics
- Chapter 2: How to conduct a Physics practical investigation
- Chapter 3: How to perform data analysis
- Chapter 4: How to write a practical report
- Chapter 5: An example depth study report on a practical investigation
What are Physics depth studies?
A depth study is any type of investigation/activity that a student completes individually or collaboratively that allows the further development of one or more concepts found within or inspired by the Physics syllabus.
The flowchart categorises different types of depth studies:
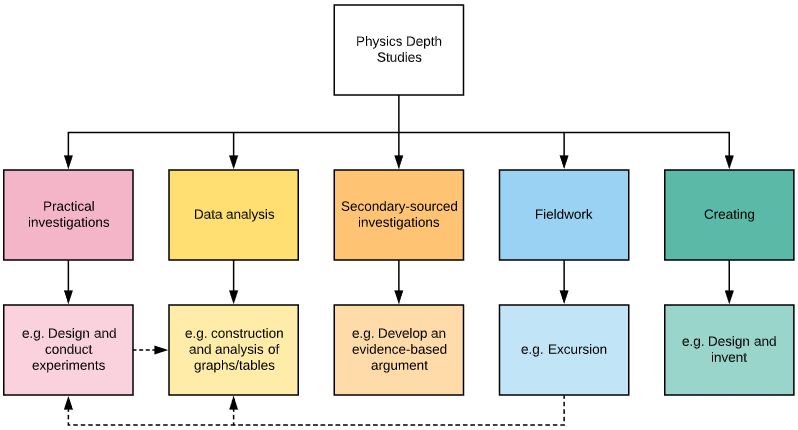
A depth study may be, but is not limited to:
- A practical investigation or series of practical investigations
- A secondary-sourced investigation or series of secondary-sourced investigations
- Presentations, research assignments or fieldwork reports
- The extension of concepts found within the course, either qualitatively and/or quantitatively
Physics depth study types and ideas
Most Physics depth studies are on:
- Practical investigations or
- Secondary-sourced investigations
A list of Physics depth study types and useful tools are provided below. For more information on each Physics depth study type, click the link.
| Depth Study Type | Ideas | Useful tools |
| Practical investigations |
|
|
| Secondary-sourced investigations |
|
|
| Data Analysis | A practical investigation, or secondary-sourced investigation may require a form of data analysis. For example:
|
|
| Creating |
| |
| Fieldwork | Fieldwork may be a starting point for a practical investigation or secondary-sourced study and could be initiated by the following stimuli:
|
Source: NSW Education Standards Authority
Four steps to choosing your Physics depth study topic
The process for completing your Physics depth study is outlined below.
| Step | Action | Detail |
| 1 | Choose the type of depth study you would like to undertake if it is not prescribed by your school. | Many schools prescribe the type of depth study that HSC Physics students will undertake. Although there are many different depth study types, most schools assign a practical investigation for their depth study assessment. |
| 2 | Choose the idea for your chosen depth study type. | NESA has provided a list of ideas for each depth study type.
|
| 3 | Choose the topic for your Physics depth study. | Once your depth study type is defined, a good place to start choosing your topic is to think about which aspect of the HSC Physics course you find most interesting and/or enjoyable. If you’re unsure of what topic you’re interested in, try scanning through the various topics in all four modules and see if anything jumps out at you. For Year 11 Physics, the modules are:
For Year 12 Physics, the modules are:
|
| 4 | Conduct your Physics depth study. | Once you have chosen the topic and type of depth study to undertake, think carefully about how you will approach and structure your work.
|
For more guidance on choosing the right Physics depth study topic, read Chapter 1: Physics Depth Study Ideas and Topics.
Are you doing a practical investigation for your depth study? Access our library of sample Physics practical reports.
Get free access to syllabus specific Physics practicals written by expert HSC teachers. Join 10000+ students who are getting ahead with Learnable. Try for free now.
Written by DJ Kim
DJ is the founder of Learnable and has a passionate interest in education and technology. He is also the author of Physics resources on Learnable.
Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.