Chapter 5: Physics Practical Investigation Report | Depth Study Example
Sample Practical Investigation Report: Module 6 Electromagnetism
The most popular type of Physics depth study in HSC Physics is a practical investigation.
The most popular idea for this depth study type is design and conduct experiments.
When designing and conducting Physics experiments, the scientific method needs to be followed. When writing a Physics practical investigation report, you should refer to Chapter 4: How to write a practical investigation report.
In this article, we share
- Sample Physics depth study assessment notification
- Sample Physics practical investigation report report
Physics practical investigation assessment notification
A sample Physics practical investigation assessment notification requiring a student to design and conduct experiment is shown below.
Task DescriptionStudents are required to develop an investigation question related to the following Physics outcome: explains and analyses the electric and magnetic interactions due to charged particles or currents and evaluates their effect both qualitatively and quantitatively.
Marking CriteriaThis task assesses skills in working scientifically involving all of the following:
This task assesses knowledge and understanding outcomes:
|
Physics practical investigation report from a Band 6 student*
*This article is shared with the author's permission.This Physics practical investigation report was written by 2019 graduate Matthew Drielsma for his depth study assessment. Matthew achieved full marks for this report and a Band 6 result in HSC Physics.
Title
An investigation to determine the value of the permittivity of free space using a parallel plate capacitor to measure the capacitance at varying distances with an applied voltage.
Inquiry question
Can we calculate the value of the permittivity of free space, ε_0 , by measuring the capacitance of two parallel plates with an applied voltage at varying distances apart?
Hypothesis
That capacitance is inversely proportional to the distance between two parallel plates and that the permittivity of free space can be calculated by measuring the capacitance between two parallel plates at varying distances with an applied voltage.
Aim
To calculate the value of the permittivity of free space, ε_0 , between two parallel plates by measuring the capacitance between the parallel plates at varying distances with an applied voltage.
Introduction
Permittivity is a measure of a medium’s tendency to resist the establishment of an electric field within it. The permittivity of free space, ε_0 , is a physical constant 8.854 \times 10^{-12} \ Fm^{-1} (farads/meter) which represents the capability of a vacuum to permit electrical fields. This value is a fundamental constant often used in the field of electromagnetism.
The electric permittivity, ε_0 , is used in the calculation of the speed of light, c ;
| c=\frac{1}{\sqrt{µ_0ε_0}} | Equation (1) |
In Coulomb’s Law, to calculate the force between two charges;
| F=\frac{q1q2}{4\pi r^2ε_0} | Equation (2) |
And in Gauss’ Law, which is the total charge of a closed surface;
| E=\frac{Q}{ε_0A} | Equation (3) |
The permittivity of free space also appears as a constant relating to capacitance, which is a measure of the ability of the capacitor to store potential energy when a current passes through it. A simple capacitor can be constructed using two parallel metal plates, with surface area (A), separated by a distance (d). The value of the permittivity of free space can be derived from the equation for capacitance (C):
| Where C=\frac{Q}{V} Where Q=charge, and V=voltage | Equation (4) |
From Gauss’ Law (3) Q=Eε_0A, substituting this into equation (4)
| C=\frac{Eε_0A}{V} | Equation (5) |
Substituting E=\frac{V}{d}, the electric field between two plates into equation (5), this allows for the expression of capacitance of parallel metallic plates:
| C=\frac{kEε_0A}{d} Where: K= Relative permittivity of the dielectric material between the plates A= Area of the plate d= Distance between the plates | Equation (6) |
The dielectric constant of a vacuum is 1.00, and for air it is close to 1.00 (1.00059) so air filled capacitors act similar to those with a vacuum. From this equation, the permittivity of free space can be determined, where capacitance is directly proportional to the area of the plates and inversely proportional to plate separation. Therefore, a straight-line graph of capacitance plotted against the inverse of plate separation distance, with constant plate area, can be used to calculate the slope. With the known plate area, the value of ε_0 can be determined from:
Slope=Aε0
| ε_0=\frac{Slope}{A} | Equation (7) |
The aim of this Physics experiment is to calculate the value of the permittivity of free space using a parallel plate capacitor to determine the relationship between capacitance and the distance of the plate separation. In calculating this value experimentally and comparing it to the known value, it will allow us to assess the experimental design and to calculate the percentage error in the measurement of ε_0 . Furthermore, when using the value of ε_0 in the future for electromagnetic equations, we are better able to understand the physics of how this value is derived and its scientific applications.
Method
Variables
Independent variable: Distance (mm) between the parallel plates
Dependent variable: Capacitance (nF) of the parallel plates
Control variables:
- Shape, size, area and material of the parallel plates
- Parallel alignment of the plates
- Voltage applied to the plates
- Multimeter
- Vernier Caliper
- Battery power source
- Ruler length and material
- Alligator clips
- Connecting wires
- Sliding Lego stand
- Temperature and humidity of the room
- Person doing the measurements
Risk Assessment
| Equipment | Potential hazard | Standard handling procedure to minimise risk |
| 1.5V C Battery | Heat released, possibly leading to rupture of case. Contents corrosive. | Check for leakage. Do not use after expiry date. |
| Multimeter | Possibility of electric shock | Do not use near water. Check for damaged cables/do not use if cables are damaged |
| Alligator clips | Can pinch skin causing pain to skin | Do not clip onto skin |
| Copper metal plates | Very sharp edges can cut skin | Take care when handling the edges of plates. |
| Scissors | Sharp blades can cut skin | Take care when handling. Store when not in use. |
| Callipers | Points on jaws may cause injury to skin and eyes if misused. | Take care when handling. Store when not in use. |
| Ruler | Metal ruler has sharp edges- can cause injury | Take care when handling |
Materials
- DC 1.5V C battery
- 2 \times (94 \ mm \times 100 \ mm) copper plates
- Digitech digital multimeter
- 4 Alligator clips
- 30 \ cm metal ruler
- Vernier caliper
- 4 Connecting wires
- Scissors
- Blue tac
- Lego sliding stand for parallel plates
Experimental setup

Procedure
- Two copper plates 0.094 \ m \times 0.10 \ m in size, were measured with a millimetre ruler and cut from a sheet of cooper.
- The copper plates were flattened under heavy books.
- The parallel copper plates were mounted, with blue tac, to a sliding stand constructed from Lego.
- A DC 1.5V C battery was connected to each of the parallel plates using connecting wires and alligator clips.
- A multimeter was set up in parallel to the plates by connecting one terminal to each plate with connecting wires and alligator clips. The multimeter was set to capacitance mode in nanofarads (nF).
- A caliper was used to measure a plate separation of 10 \ mm .
- The capacitance reading on the multimeter was recorded. The multimeter was immediately turned off.
- Steps 6-7 were repeated using plate separations of 20 \ mm, 30 \ mm, 40 \ mm, 50 \ mm, 60 \ mm, 70 \ mm .
- Three trials were completed for each plate separation and the values for capacitance were averaged.
- The inverse distance in was calculated.
- Using Excel, a graph of the capacitance C (F) was plotted against the inverse of the distance between the parallel copper plates d^{-1} (m^{-1}) .
Results
Data table
| Distance between plates (mm) | 1/d (m^{-1}) | Capacitance (nF) | Capacitance (F) | |||
| Trial 1 | Trial 2 | Trial 3 | Average | |||
| 10 | 100 | 0.033 | 0.033 | 0.032 | 0.033 | 3.3 x 10-11 |
| 20 | 50.0 | 0.024 | 0.024 | 0.024 | 0.024 | 2.4 x 10-11 |
| 30 | 33.3 | 0.021 | 0.021 | 0.022 | 0.021 | 2.1 x 10-11 |
| 40 | 25.0 | 0.020 | 0.019 | 0.019 | 0.019 | 1.9 x 10-11 |
| 50 | 20.0 | 0.018 | 0.019 | 0.018 | 0.018 | 1.8 x 10-11 |
| 60 | 16.7 | 0.017 | 0.018 | 0.017 | 0.017 | 1.7 x 10-11 |
| 70 | 14.3 | 0.015 | 0.018 | 0.016 | 0.016 | 1.6 x 10-11 |
Discussion
Quantitative analysis
The results were plotted and the line of best fit was drawn to display the relationship between capacitance and inverse distance for the parallel plate capacitor as shown below.
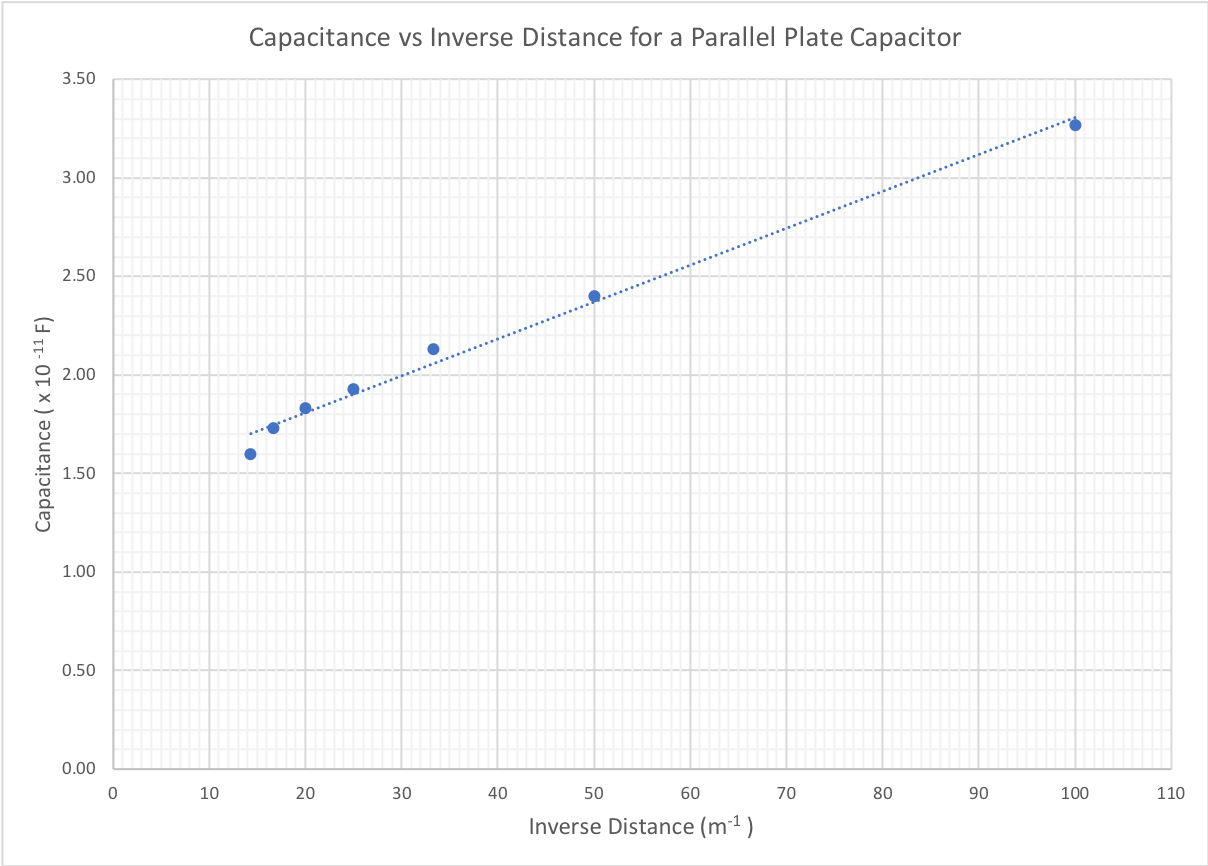
Using the slope of the line of best fit and the area of the plates, the permittivity of free space ε_0 was calculated.
Slope=Aε_0
Slope=\frac{Δy}{Δx}=2.0 \times 10^{-13} \ Fm
ε_0=\frac{Slope}{A}
ε_0=\frac{2.0 \times 10^{-13}}{0.0094}
\therefore ε_0=2.13 \times 10^{-11} \ Fm^{-1}
Qualitative analysis
Assessment of whether and how the questions raised in the introduction (aim) have been answered:
The aim of this experiment was to calculate the value of the permittivity of free space, ε_0 , by measuring the capacitance between two parallel plates at varying distances with an applied voltage. The values of capacitance were plotted against the inverse distance between the plates, the slope was determined from the line of best fit. The slope was then used to calculate ε_0 .
A capacitor was made using two parallel copper plates separated by a certain distance. When a voltage was applied, a uniform electric field was created between the plates. From the establishment of this electric field the capacitance was able to be measured. As capacitance is proportional to inverse distance, a graph of capacitance vs inverse separation of the plates resulted in a straight line of best fit, consistent with other sources found in research (Reyes, 2015). The slope of this line was calculated to be 2.0 \times 10^{-13} \ Fm (Figure 3). From this calculation of slope, the value of the permittivity of free space was derived using the area of the plates (Equation 7). The experimental value obtained of 2.13 \times 10^{-11} \ Fm^{-1} , does not agree with the accepted value of 8.854 \times 10^{-12} \ Fm^{-1} with an experimental error of 40.6%.
Evaluation of the method and sources of error in the experiment:
Systematic sources of error in the experimental design have resulted in the discrepancy between the measured and theoretical value for the permittivity of free space.
The accepted value of 8.854 \times 10^{-12} \ Fm^{-1} was calculated in a vacuum, however the experimental value was obtained in air, which has humidity that would affect the charge between the parallel plates, thus affecting the calculation. Water is a polar molecule and in the presence of an electric field between two charged plates, the molecules align with the charges on the plate opposing the electric field and thus the net electric field is reduced which increases capacitance (Al-Ta’ii, Amin & Periasmy, 2016). Thus, the humidity of the air has contributed to the systematic error. The dielectric constant of a vacuum is 1.00, which was used in the calculation, and air is 1.00059, so in effect this is a systematic error which will slightly increase the measured value of permittivity of free space.
Furthermore, the alignment of the two plates were not completely parallel since the plates were mounted with blue tac and had dents from trying to straighten them out, this would significantly contribute to a systematic error since there was not a uniform electric field between the plates which would affect the value of capacitance. These systematic errors can be seen in the y-intercept of the graph (Figure 3) which has occurred due to the values of capacitance being shifted up by a fixed value.
Identification and justification of improvements to the experiment in relation to accuracy, reliability and validity
Reliability:
Reliability is the consistency of the results. The method was reliable in that there were three repeats at each distance between the plates and the results were reliable as the results obtained were consistent in each trial (Table 1) and there was not much deviation from the line of best fit. The results were averaged, and the average was plotted on the graph
Validity:
Validity is an assessment of how well the experiment meets the aim. This experiment was not valid in that not all variables were able to be controlled and kept constant. The plates were not completely parallel as they were cut from a rolled sheet of copper which was difficult to flatten without leaving dents in them. Also, they were mounted on a Lego stand held in place with blue tac, which further contributed to their lack of precise parallel alignment. Variables that were kept constant included, the shape, size, area, thickness and material of the plates, the voltage applied between the plates, the multimeter, battery, ruler, calliper, alligator clips, temperature and humidity of the room and the person doing the measurements. Only the distance between the parallel plates (independent variable) was varied.
Accuracy:
Accuracy is a measure of how close the experimental results are to the accepted true value.
- The calculated result for ε0 in this experiment was 2.13 \times 10^{-11} \ Fm^{-1}
- The accepted true value for ε_0 is 8.854 \times 10^{-12} \ Fm^{-1}
The percentage error for this experiment is given by:
\% \ error=\frac{|true-experimental|}{true} \times 100
\therefore \% \ error=\frac{|8.854 \times 10^{-12}-2.13 \times 10^{-11}|}{8.854 \times 10^{-12}} \times 100=40.6\%
The experimental value calculated for the permittivity of free space was 2.13 \times 10^{-11} \ Fm^{-1} which resulted in an experimental error which was 1.41 times the theoretical value, a 40.6% error compared to the known value of 8.854 \times 10^{-12} \ Fm^{-1} thus, this experiment was not accurate.
Research of a secondary source (Reyes, 2015) revealed a more accurate value in the calculation of the permittivity of free space. In carrying out 3 repeats for each separation distance with the use of precision instruments such as a digital caliper, capacitance meter and a horizontal parallel plate set up using disc spacers to separate the plates ensured this experiment was valid with greater accuracy in the value obtained for ε_0 of 9.62 \times 10^{-12} \ Fm^{-1} with an error of only 8.70%.
How to improve or extend the experiment:
To improve this experiment, the use of a factory made variable parallel plate capacitor set up, where the plates could be adjusted to ensure they were precisely parallel and where a sliding measurement bar was present to give precision distance, would significantly improve validity and accuracy.
Furthermore, the use of a laser distance sensor would increase the accuracy and the precision for small distances between the plates and performing this experiment in a vacuum would eliminate any humidity and air particles and thus increase the validity and accuracy.
To extend this experiment, it would be interesting to determine the effect of placing different materials between the charged parallel plates, such as paper, plastic and glass, all of which have different dielectric coefficients (k) that are greater than air . The determination of the effect on capacitance compared to air can be calculated using equation (6) and gives insight into how these materials are used in real life applications such as making efficient capacitors.
Conclusion
Using a constant voltage, the capacitance of parallel plates was measured at varying separation distances and plotted against the inverse distance. From the slope of the line of best fit, the permittivity of free space, ε0,was calculated. The experimental value obtained was 2.13 \times 10^{-11} \ Fm^{-1} with a 40.6% error compared to the theoretical value of 8.854 \times 10^{-12} \ Fm^{-1} . This error can be attributed to multiple systematic errors in the experimental method and uncertainties in the measurements. This experiment was reliable but not valid, thus, the hypothesis was not supported by the experimental data obtained.
References
Al-Ta’ii, H., Amin, Y., Periasmy. (2016). Humidity influenced capacitance and resistance of an Al/DNA/Al Schottky diode irradiated by alpha particles. Scientific reports. Retrieved from https://www.nature.com/articles/srep25519
Anderson, P. (2014, June 10). Bozeman Science. Physics Essentials 19 Electric Permittivity. [Video File]. Retrieved from https://www.youtube.com/watch?v=5x8kj02ar34
Bevelacqua, P. (2012). Maxwell’s Equations. Permittivity. Retrieved from http://maxwells-equations.com/materials/permittivity.php
Ecosolve Australia. (2019). Risk Assessment for Schools. Retrieved from https://www.riskassess.com.au/
Farr, R., Wilson, K., Philip, Y., Gossens, D. (2018). Physics in Focus Year 12. Cengage Learning Australia, Victoria.
Gibbs, K. (2013). School Physics. The parallel plate capacitor. Retrieved from http://www.schoolphysics.co.uk/age16-19/Electricity%20and%20magnetism/Electrostatics/text/Capacitors_parallel_plate/index.html
Gyorki, J. (2010). How to determine Digital Multimeter Accuracy. Retrieved from https://www.designworldonline.com/how-to-determine-digital-multimeter-accuracy/
Hosch, W. (2019). Encyclopedia Britannica. Permittivity. Retrieved from https://www.britannica.com/science/permittivity
JM Donev et al. (2018). Energy Education – Permittivity of free space. Retrieved from https://energyeducation.ca/encyclopedia/Permittivity_of_free_space
Mass, E. (1998). What is Electric permittivity of free space and how is it calculated? Retrieved from http://www.madsci.org/posts/archives/1998-03/889017173.Ph.r.html
Nave, R. (2016). hyperphysics. Electric field. Retrieved from http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elefie.html
Open Stax College Physics., (2012). Capacitors and Dielectrics. Retrieved from https://opentextbc.ca/physicstestbook2/chapter/capacitors-and-dielectrics/
Reyes, E. (2015) Measuring Permittivity of Free Space. Retrieved from https://www.studocu.com/en/document/university-of-arkansas/univ-physics-ii/mandatory-assignments/measuring-permittivity-of-free-space-up11-lab-1-elio-reyes-imprimir/1210918/view
Skitka, J., Albright, S. (2014). Brown Physics. The Permittivity of Free Space. Retrieved from https://wiki.brown.edu/confluence/download/attachments/1163909/Electric%20Fields.pdf?version=1&modificationDate=1438368000000&api=v2
Access our library of Physics practical investigation reports for your depth study.
Get free access to syllabus specific Physics practicals written by expert HSC teachers. Join 10000+ students who are getting ahead with Learnable. Try for free now.
Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.
