Test your exam readiness for HSC Physics Module 5
HSC Physics Module 5 demands students demonstrate a high level of competency in their skills, knowledge and understanding of:
- The analysis of forces acting on a system, and
- The energy transformations that take place within and around the system.
The concepts covered in HSC Physics Module 5 Advanced Mechanics are an extension of the foundational concepts taught in Year 11 Physics Module 2 Dynamics.
The key to acing HSC Physics Module 5 begins with having a solid understanding of all the Physics concepts in Module 2.
In this article, we reveal:
- 7 commonly asked question types from HSC Physics Module 5.
- 10 Must Know Questions to ace your next HSC Physics Module 5 Exam.
What are commonly asked exam question types in HSC Physics Module 5?
7 commonly asked question types from the HSC Physics Module 5 Advanced Mechanics syllabus are listed below:
| NESA Content Block | Question Type |
| Projectile Motion | - Analysing the motion of projectiles in a variety of situations.
|
| Circular Motion | - Analysing uniform circular motion involving:
- Cars on banked tracks
- Conical pendulum
- Motion in a vertical plane
- Analysing quantitatively and qualitatively the non-uniform circular motion of objects.
|
| Motion in Gravitational Fields | - Calculating the gravitational acceleration of objects.
- Analysing quantitatively the orbital motion of planets and artificial satellites using Kepler’s Laws.
- Calculating the total energy of a planet or satellite in its orbit.
- Calculating energy changes that occur when satellites move between orbits.
|
Source: NESA website
10 Must Know Questions for HSC Physics Module 5
Question 1 (4 marks)
Planet Z has twice the mass and twice the radius of the Earth.
| (a) | Derive an expression for the magnitude of the gravitational acceleration on the surface of Planet Z in terms of the gravitational acceleration on the surface of the Earth, g. | 2 |
| (b) | A 10 kg object rests on a horizontal plane at the surface of Planet Z. Calculate the force exerted on the object by the surface. | 2 |
See Question 1 Solution
Question 2 (5 marks)
A golfer hits a hole-in-one by just clearing a tree situated in front of them. The tree is 4.9 m tall as shown below.
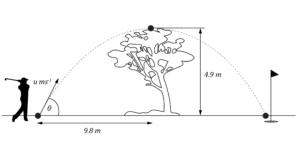
Assume the acceleration due to gravity is g = 9.8 \ ms^{-2} .
| (a) | With what vertical component of initial velocity must the golfer hit the ball so that it will just pass over the top of the tree? | 2 |
| (b) | How long will it take the ball to travel the horizontal distance of 9.8 \ m ? | 1 |
| (c) | At what angle to the horizontal did the golfer hit the ball? | 2 |
See Question 2 Solution
Question 3 (6 marks)
A ball of mass m is attached to a string and travels at constant speed in a horizontal circle as shown. The string makes an angle of \theta \degree with the vertical axis.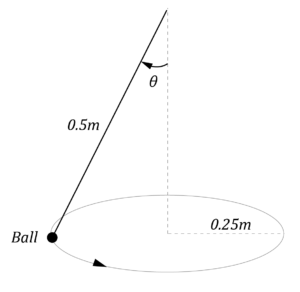
| (a) | State the direction of the net force acting on the rotating mass. Give a reason for your answer. | 2 |
| (b) | Show that the acceleration of the ball is given by a = g tan \theta . | 2 |
| (c) | If the ball has a mass of 50 \ g , calculate the magnitude of the acceleration and the tension in the string. Express your answer to 2 significant figures. | 2 |
See Question 3 Solution
Question 4 (5 marks)
The London Eye is the fourth largest Ferris wheel in the world. The wheel has a radius of 135 m and rotates once every 30 minutes. A schematic representation of the London Eye is shown below.
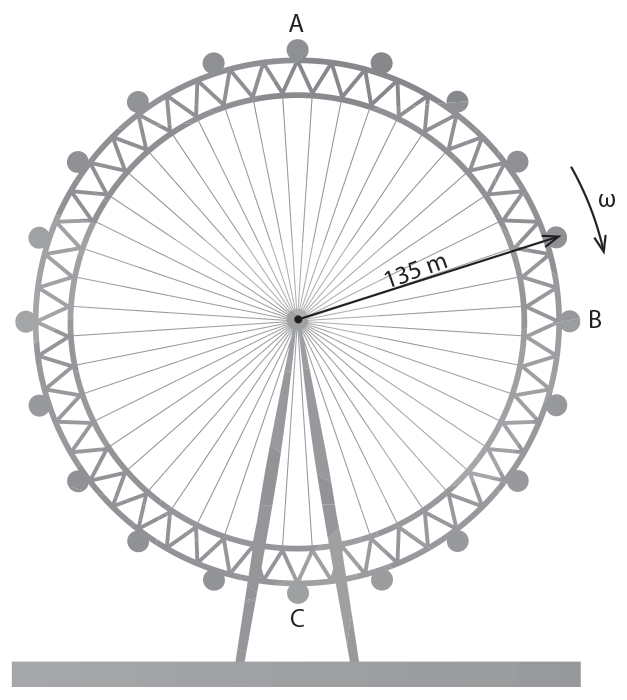
| (a) | At which position, A, B or C, is the net force acting on the passenger sitting inside a capsule the greatest?. Give a reason for your answer. | 2 |
| (b) | Calculate the normal force acting on a 70 kg passenger sitting inside a capsule when it is at position C, the bottom of the Ferris wheel. Express your answer to two significant figures. | 3 |
See Question 4 Solution
Question 5 (7 marks)
A car is travelling along a road when it reaches a bend. The bend is horizontally flat, follows a circular arc and has a radius of 25.6 \ m . The car and its occupants have a combined mass of 885 \ kg , and the force of kinetic friction between the tyres and the road is 9420 \ N .
| (a) | What is the maximum speed at which the car can travel around the bend? | 2 |
| (b) | Hence explain quantitatively why motorists are advised to travel at slower speeds in wet weather. | 3 |
| (c) | In the interests of public safety, bends in roads are often built to be banked toward the inside of the turn, such that the flat road surface forms an angle to the horizontal. If the road bend in part (a) was banked at 6 \degree , describe qualitatively how this increases the maximum speed at which the turn can be successfully travelled. | 2 |
See Question 5 Solution
Question 6 (7 marks)
A loop-de-loop track is shown below. The loop in the track has a radius of 39.2 \ m .
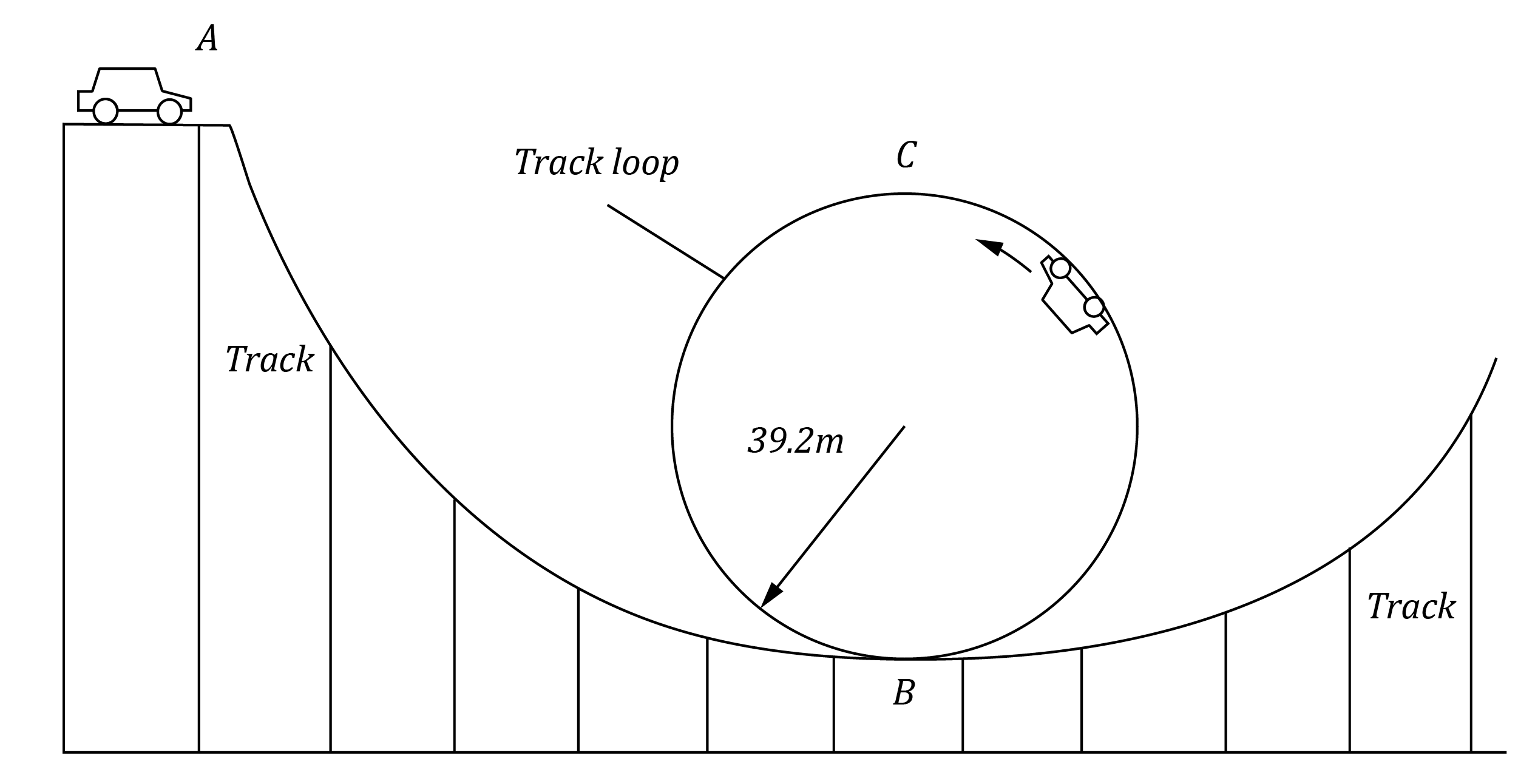
In order to complete the loop-de-loop successfully, the car must not lose contact with the track when travelling around the top of the loop, at point C. Ignore the effects of air resistance and friction.
| (a) | Calculate the minimum speed that the car and driver must have at point C so that the car does not lose contact with the track. | 3 |
| (b) | Calculate the required speed of the car when entering the bottom of the loop, at point B. | 2 |
| (c) | Calculate the minimum height h of point A above point B that will ensure the car and driver successfully complete the loop-de-loop. | 2 |
See Question 6 Solution
Question 7 (4 marks)
The orbit of Halley’s comet is shown below.
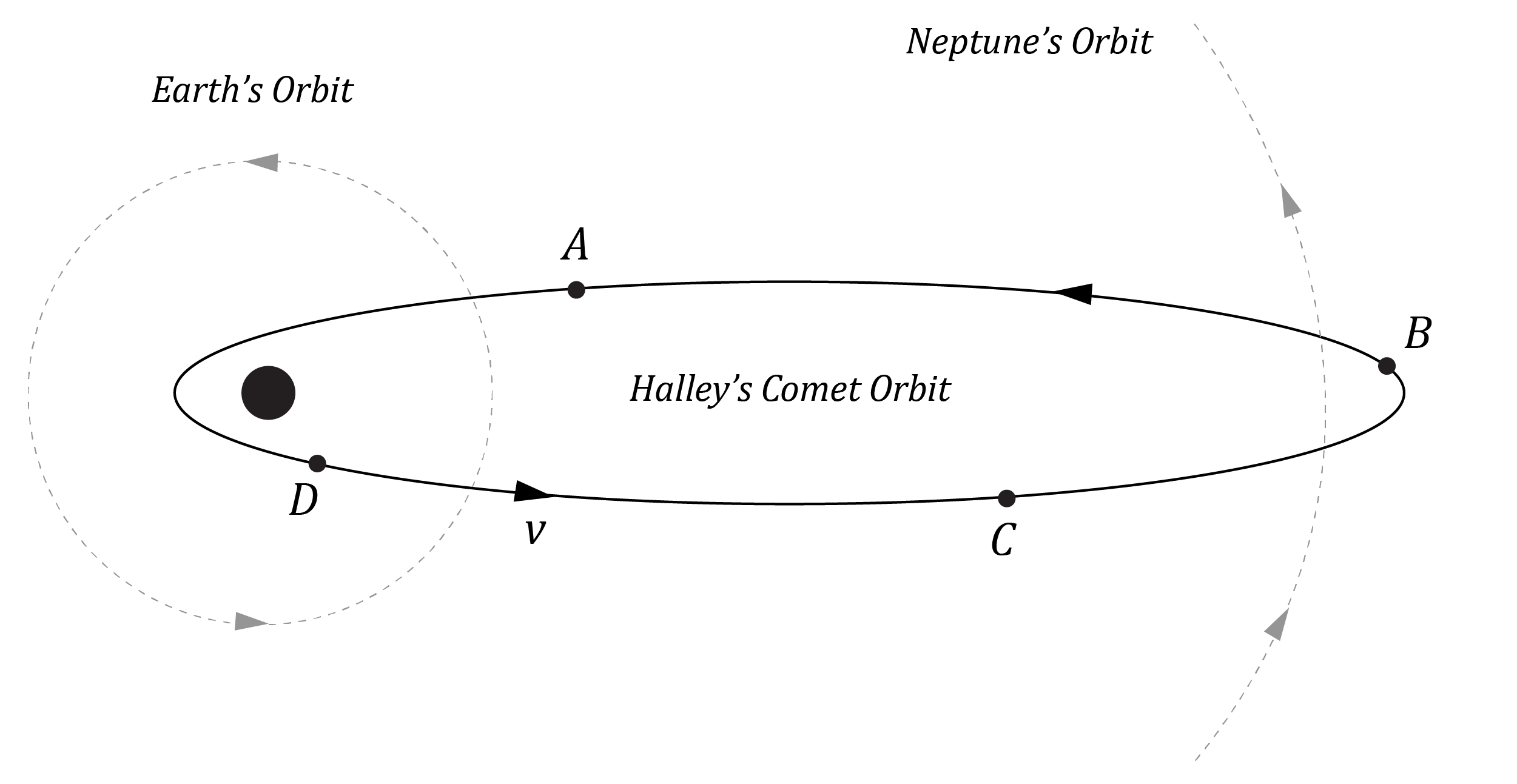
Halley’s Comet has a mass of 2.2 \times 10^{14} \ kg , and the Sun has a mass of 1.989 \times 10^{30} \ kg .
| (a) | At which position along its orbit (A, B, C or D) is Halley’s Comet moving the slowest? Justify your answer by making reference to an appropriate equation. | 2 |
| (b) | Calculate the constant K , in SI units, for Halley’s Comet. | 2 |
See Question 7 Solution
Question 8 (4 marks)
A 1000 \ kg geostationary Earth satellite is moved to a smaller orbital radius of 6 \ 600 \ km .
Calculate the work done in changing the satellite’s orbit. Express your answer to two significant figures.
See Question 8 Solution
Question 9 (3 marks)
Escape velocity is the minimum initial projectile velocity needed by an object to escape the gravitational field of a body in space, when starting at a given distance from that body.
| (a) | Using the Law of Conservation of Energy, derive an expression for the escape velocity on Earth. | 2 |
| (b) | Hence calculate the magnitude of the escape velocity from Earth for a 10 \ 000 \ kg spacecraft. Express your answer to three significant figures. | 1 |
See Question 9 Solution
Question 10 (5 marks)
An experiment is conducted to investigate the relationship between weight and mass on the surface of the moon.
The collected data is plotted on a graph of weight (N) vs mass (kg) .
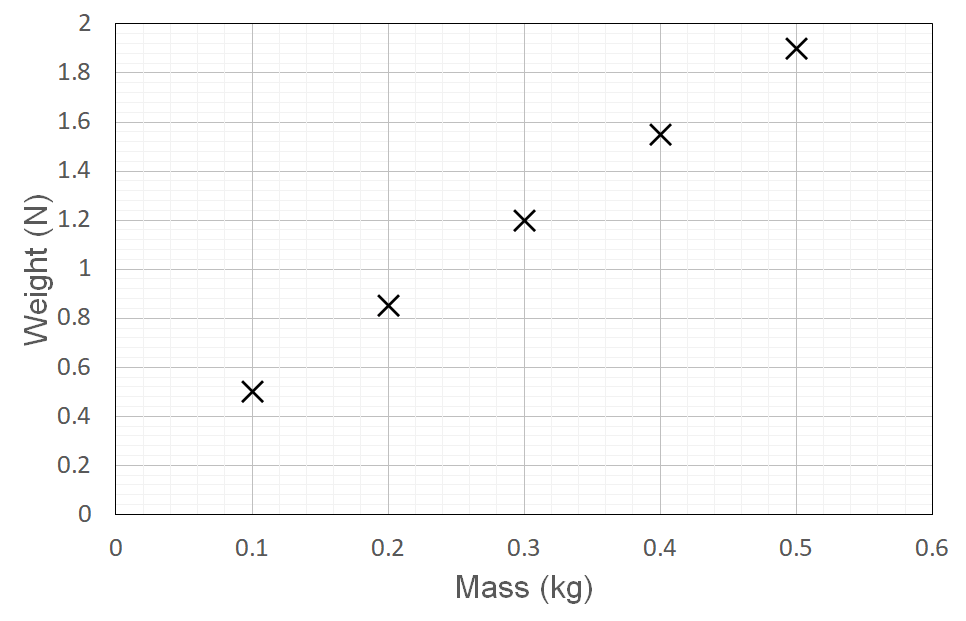
| (a) | Using the experimental results, calculate the gravitational acceleration on the moon. | 3 |
| (b) | The actual value for the gravitational acceleration on the moon is 1.62 \ ms^{-2} . Calculate the accuracy of the experiment to three significant figures. | 2 |
See Question 10 Solution
Solutions to HSC Physics Module 5 Questions
Detailed step-by-step solutions to the Module 5 Advanced Mechanics questions are provided below.
| Question | Solution |
| 1 | Part (a): At the surface of the Earth: \begin{aligned} mg &= \dfrac{GM_{_{E}} m}{r^2_{_{E}}} \\\\ \therefore g &= \dfrac{GM_{_{E}}}{r^2_{_{E}}} \end{aligned} At the surface of Planet Z: \begin{aligned} g_{_{Z}} &= \dfrac{G (2M_{_{E}}) }{ (2r_{_{E}})^2 } \\\\&= \dfrac{1}{2} \dfrac{ GM_{_{E}} }{ r^2_{_{E}}} \\\\ &=\dfrac{g}{2} \end{aligned} Hence, the gravitational acceleration on the surface of Planet Z is equal to half the gravitational acceleration on the surface of the Earth (\dfrac{g}{2}) . Part (b): The force with which the surface acts on the object is the normal force. This is a reaction to the component of weight force acting into the surface. In this case with a horizontal surface the normal force is equal in magnitude to the weight force of the non-accelerating (resting) object. \begin{aligned} N &= W \\ &= mg_{_{Z}} \\&=10 \times \dfrac{9.8}{2} \\&= 49 \ N \end{aligned} Back to Question 1 |
| 2 | Part (a): Step 1: Identify the given data in SI units. - s_y = 4.9 \ m
- a_y = -9.8 \ ms^{-2}
Step 2: Use a characteristic of projectile motion, and an appropriate equation, to calculate the initial vertical velocity of the golf ball. At maximum height, v_y = 0 \begin{aligned} v^2_y &= u^2_y + 2a_y s_y \\ 0 &= u^2_y + 2(-9.8)(4.9) \\ \therefore u^2_y &= 2(9.8)(4.9) \\ u_y &= 9.8 \ ms^{-1} \end{aligned} Part (b): The time taken for the ball to travel the horizontal distance of 9.8 \ m is the same as the time take to reach maximum height. At maximum height v_y = 0 . Using u_y = 9.8 \ ms^{-1} from part (a): \begin{aligned} v_y &= u_y + a_y t \\ 0 &= 9.8 - 9.8t \\ t &= 1 \ s \end{aligned} Part (c): Step 1: Calculate the initial horizontal velocity of the golf ball u_x . From part (b) we know that it takes 1 \ s to travel the horizontal distance of 9.8 \ m . Therefore: \begin{aligned} s_x&=u_xt \\ \therefore u_x &= \frac{s_x}{t} \\ &= \frac{9.8}{1} \\ &= 9.8 \ ms^{-1} \end{aligned} Step 2: Find the angle by constructing a vector diagram that consists of u_x and u_y : 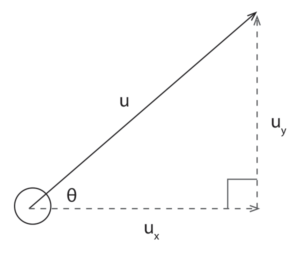
\begin{aligned} \tan \theta &= \dfrac{ u_y }{ u_x } \\ &= \dfrac{9.8}{9.8} \\ \therefore \theta &= \tan^{-1}(1) \\ &= 45 \degree \end{aligned} Back to Question 2 |
| 3 | Part (a): The net force on the ball is acting toward the centre of the horizontal circle. This is because the ball is undergoing uniform circular motion in the horizontal plane, so the net force on the ball is a centripetal force. Part (b): Step 1: Identify the forces acting on the object. - Tension (T)
- Weight force (mg)
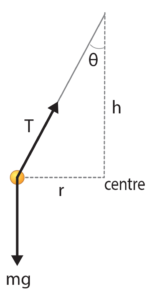
Step 2: Decompose the forces into horizontal (x) and vertical components (y). This ensures forces are either parallel or perpendicular to the centripetal acceleration. Weight force is already perpendicular to the acceleration. T_x=T\sin\theta and T_y=T\cos\theta Step 3: Apply Newton’s Second Law \Sigma F = m a_y separately to the components of force that are parallel and perpendicular to the acceleration, then find an expression for the acceleration. Perpendicular to acceleration is the vertical axis in which there is no acceleration, so for \Sigma F_y = m a_y :
\begin{aligned} T\cos\theta - mg &= ma_y \\ T\cos\theta - mg &= 0 \\ T\cos\theta &= mg \\ T &= \frac{mg}{\cos\theta} \end{aligned} Parallel to acceleration is the horizontal axis where a_x = a_c = a , so for \Sigma F_x = ma_x :
\begin{aligned} T\sin\theta &= ma_x \\ &= ma \end{aligned} Substituting T = \frac{mg}{\cos\theta} into the expression for \Sigma F_x : \begin{aligned} T \sin \theta &= ma \\ \frac{mg \sin \theta}{\cos \theta} &= ma \\ \therefore a &= g \tan \theta \end{aligned} Part (c) Step 1: Identify the given data in SI units - l = 0.5 \ m
- r = 0.25 \ m
- m = 0.05 \ kg
Step 2: Use a = g \tan \theta to calculate the acceleration and then the tension in the string. \begin{aligned} \sin \theta &= \frac {r}{l} \\ &=\frac{0.25 \ m}{0.5 \ m} \\ \therefore \theta&=30 \degree \end{aligned} \begin{aligned} a &= g\tan\theta \\ &= 9.8 \times \tan 30\degree \\ &= 5.6580... \\ &= 5.7 \ ms^{-2} \end{aligned} \begin{aligned} T &= \dfrac{mg}{\cos \theta} \\ &= \dfrac{0.05 \times 9.8}{\cos 30\degree} \\ &=0.5658.. \\ &=0.57 \ N \end{aligned} Back to Question 3 |
| 4 | Part (a) The net force on the passenger at positions A, B and C is the same. The Ferris wheel is a rigid body that undergoes uniform circular motion. Therefore the acceleration of the passenger is centripetal acceleration, the magnitude of which remains constant throughout the circular motion. Since the magnitudes of passenger mass and acceleration have constant magnitude, then the net force on the passenger also has constant magnitude throughout the circular motion. Part (b) Step 1: Derive an expression for the normal force acting on the passenger at the bottom of the Ferris wheel. There are only two forces acting on a passenger at position C, the bottom of the Ferris wheel, and both act in the vertical axis: - Normal force N acting upwards, and
- Weight force mg acting downwards.
These two forces combine to yield a net force on the passenger, which is a centripetal force causing uniform circular motion. At position C this centripetal (net) force is directed upward (toward the centre of the circular motion). Taking up as the positive direction, the sum of the above two forces allows the normal force on the passenger N to be calculated: \begin{aligned} F_{net} &= ma \\ N - mg &= ma \\ N &= mg + ma \end{aligned} Step 2: Utilise the given data, and the expression obtained in Step 1, to calculate the normal force acting on the passenger at the bottom of the Ferris wheel. \begin{aligned} N &= m (g + a) \\ &= m (g + r \omega ^2 ) \\ &= 70 \bigg(9.8 + 135 \times \bigg( \dfrac {2 \pi }{ 30 \times 60} \bigg) ^2 \bigg) \\ &=686.11.. \\&=690 \ N \end{aligned} Back to Question 4 |
| 5 | Part (a): In this scenario the road-tyre friction f is acting as the centripetal force causing uniform circular motion. Hence, we can rearrange the formula for centripetal force to make velocity the subject: \begin{aligned} F = f &= \dfrac{mv^2}{r} \\ \therefore v &= \sqrt \dfrac{fr}{m} \end{aligned} Substituting the given values for radius, mass and frictional force yields the maximum velocity at which the car and its occupants can successfully travel around the bend: \begin{aligned} v &= \sqrt \dfrac{fr}{m} \\ &= \sqrt \dfrac{ 9420 \times 25.6}{ 885 } \\ &= 16.5072... \\ &= 16.5 \ ms^{-1} \ (3 \ s.f.) \end{aligned} Part (b): The maximum velocity at which the car can successfully travel around the bend is dependent upon the maximum road-tyre friction force (f) as per the expression: v = \sqrt \frac{fr}{m} . That friction force is given by f = \mu_{_K}N , where N is the normal force acting on the vehicle and \mu_{_K} is the road-tyre coefficient of kinetic friction. In wet weather, meaning with water on the road, the road-tyre coefficient of kinetic friction is decreased compared to dry weather conditions. This reduces the maximum amount of road-tyre friction. Hence with f \lt 9420 \ N therefore v \lt \sqrt \frac{fr}{m} , so v \lt 16.5 \ ms^{-1} . Drivers must slow down to successfully travel around the bend in wet weather. Part (c): On a banked turn there is a component of normal force N acting horizontally N_x = N \sin \theta and contributing to the centripetal force. Consequently, there is reduced reliance on friction to fully supply the centripetal force. Hence if the friction and horizontal component of normal force are combined, this would allow a higher possible speed at which the car can successfully travel around the banked turn. Back to Question 5 |
| 6 | Part (a): At the top of the loop-de-loop: \begin{aligned} F_c &= ma_c \\ N+mg &= ma_c \end{aligned} The minimum velocity v at the top occurs when the centripetal force F_c is a minimum. This occurs when the normal force N is zero and the centripetal force is comprised solely of the weight force mg : \begin{aligned} mg &= ma_c \\ mg &= \frac{mv^2}{r} \\ g &= \frac{v^2}{r} \\ v &= \sqrt{rg} \\ &= \sqrt{39.2 \times 9.8} \\ &= 19.6 ms^{-1} \end{aligned} Part (b): By the Law of Conservation of Energy, the mechanical energy is the same at the top and the bottom of the loop: \begin{aligned} E_{_{B}} &= E_{_{C}} \\\\ K_{_{B}} + U_{_{B}} &= K_{_{C}} + U_{_{C}} \\\\ \frac{1}{2} mv_{_{B}}^2 + mgh_{_{B}} &=\frac{1}{2} mv_{_{C}}^2+mgh_{_{C}} \\\\ \frac{1}{2} v_{_{B}}^2 + 0 &= \frac{1}{2} (gr)+g(2r) \\\\ v_{_{B}}^2 &= gr+4gr \\\\ v_{_{B}} &= \sqrt{5gr} \\\\ &= \sqrt{(5)(9.8)(39.2)} \\\\ &=43.826... \\\\ &=43.8 \ ms^{-1} \end{aligned} Part (c): The potential energy at point A ( U_{_{A}} = mgh_{_{A}}) is converted into the kinetic energy at point B (K_{_{B}} = \frac{1}{2} mv^2_{_{B}} ) . We require U_{_{A}} = K_{_{B}} such that v_{_{B}} = \sqrt{5gr} : \begin{aligned} mgh_{_{A}} &= \frac{1}{2} mv_{_{B}}^2 \\\\ gh_{_{A}} &= \frac{1}{2}\times 5gr \\ \\ h_{_{A}} &= \frac{5r}{2} \\\\ &= \frac{5 \times 39.2}{2} \\\\ &= 98 \ m \end{aligned} Back to Question 6 |
| 7 | Part (a): According to Kepler’s Law of Equal Areas (second law), Halley’s comet is moving the slowest when it is furthest away from the Sun. Therefore, of the four positions indicated it is moving the slowest at position B. This can be shown with the conservation of angular momentum (L = mvr) between any two points in the comet’s orbital motion: \begin{aligned} L_{_{B}} &= L_{_{D}} \\\\ mv_{_{B}}r_{_{B}} &= mv_{_{D}}r_{_{D}} \\\\ \therefore v_{_{B}} &= \frac{v_{_{D}}r_{_{D}}}{r_{_{B}}} \end{aligned} Thus at a larger distance r the velocity v is less. Part (b): From Kepler’s Law of Periods (third law), the constant K is given by K = \dfrac{r^3}{T^2} , which when combined with Newtonian gravity gives \dfrac{r^3}{T^2} = \dfrac{GM}{4\pi^2} , such that K = \dfrac{GM}{4\pi^2} . The mass M is the mass of the central body, so substituting the mass of the Sun yields: \begin{aligned} K &= \frac{ GM_{Sun} }{ 4 \pi ^2 } \\\\ &= \frac{ 6.67 \times 10^{-11} \times 1.989 \times 10^{30} }{4 \pi ^2 } \\\\ &= 3.36 \times 10^{18} \ m^3 s^{-2} \end{aligned} Back to Question 7 |
| 8 | Step 1: Identify the given data in SI units.- m = 1000 \ kg
- r_i = ?
- r_f = 6.6 \times 10^6 \ m
Step 2: Determine the radius of the geostationary orbit using Kepler’s Third Law, where one day (one orbit) is 24 hours. \begin{aligned} \frac{r^3}{T^2}&=\frac {GM_{Earth}}{4 \pi^2}\\ \frac{r^3}{(24 \times 60 \times 60)^2}&=\frac {6.67 \times 10^{-11} \times 6.0 \times 10^{24}}{4 \pi^2} \\ r^3&=(24 \times 60 \times 60)^2 \times \frac {6.67 \times 10^{-11} \times 6.0 \times 10^{24}}{4 \pi^2} \\ r&=42297523.87 \space m \\ r&=4.23 \times 10^7 m \end{aligned} Step 3: Calculate the energy required to move the satellite from the geostationary earth orbit to the lower altitude orbit. The work required is equivalent to the change in total mechanical energy (E = -\frac{GMm}{2r}) between the two orbits: \begin{aligned} \Delta E &= \dfrac{ GMm }{ 2 } \bigg( \frac{1}{r_i} - \frac{1}{r_f} \bigg) \\ &= \frac{ 6.67 \times 10^{-11} \times 6.0 \times 10^{24} \times 1000}{2} \bigg( \frac{1}{4.23 \times 10^{7}} - \frac{1}{6.6 \times 10^6} \bigg) \\ &= -2.5587... \times 10^{10} \\ &= -2.6 \times 10^{10} \ J \ (2 \ s.f.) \end{aligned} Back to Question 8 |
| 9 | Part (a): The Law of Conservation of Energy can be used to find the minimum value of the initial speed such that the object will escape the Earth’s gravitational field. This is because total mechanical energy in this system remains constant: \dfrac{1}{2} mv^2_i - \dfrac{GMm}{r_i} = \dfrac12mv^2_f - \dfrac{GMm}{r_f} However, for the minimum velocity to escape: - The initial conditions are that the object is at the surface of the Earth (r_i = r_{_{E}}) , with initial velocity equal to escape velocity (v_i = v_{esc}) .
- The final conditions are that the object has reached a distance where the gravitational force is reduced to zero (r_f = \infty) and that it has zero velocity at this distance (v_f = 0) .
Substituting these conditions into the above equation for the conservation of mechanical energy yields: \begin{aligned} \frac12 mv^2 _{esc} - \frac{GMm}{r_{_{E}}} &= \frac12 m (0)^2 - \frac{GMm}{\infty} \\\\ \frac12 mv^2_{esc} - \frac{GMm}{r_{_{E}}} &= 0 \\\\ \frac12 mv^2_{esc} &= \frac{GMm}{r_{_{E}}} \\\\ \frac12 v^2 _{esc} &= \frac{GM}{r_{_{E}}} \\\\ \therefore v_{esc} &= \sqrt \frac{2GM}{r_{_{E}}} \end{aligned} Part (b): Using the formula for escape velocity derived in part (a): \begin{aligned} v_{esc} &= \sqrt{ \frac{ 2GM_{_{E}} }{ r_{_{E}} } } \\\\ &= \sqrt{ \frac{ 2 \times 6.67 \times 10^{-11} \times 6.0 \times 10^{24} }{ 6.371 \times 10^6} } \\\\ &= 11208.55 ... \\\\ &= 1.12 \times 10^4 \ ms^{-1} \ (3 \ s.f.) \end{aligned} Back to Question 9 |
| 10 | Part (a): Step 1: Draw a line of best fit across the given data. 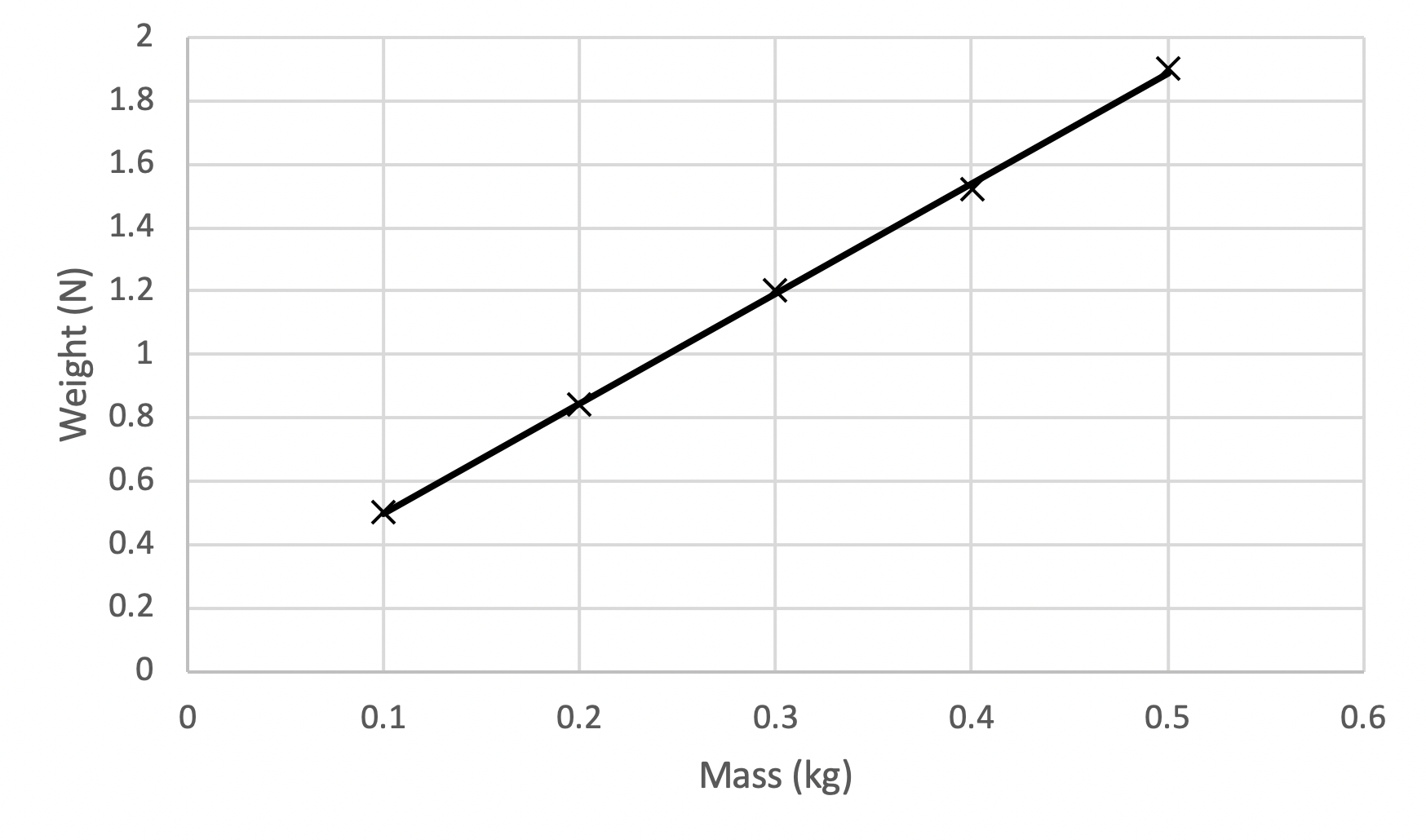
Step 2: Calculate the gradient of the line of best fit. To calculate the gradient of the line of best fit, we use the equation gradient = m = \frac{rise}{run} : \begin{aligned} m &= \frac{rise}{run} \\\\ &= \frac{1.7 - 1}{0.45 - 0.24} \\\\ &= 3.33 \end{aligned} Step 3: Identify what the gradient of the graph represents. The graph plots Weight vs Mass. Hence the gradient is equivalent to \frac{rise}{run} = \frac{mg}{m} = g . The units are Newtons per Kilogram. These SI units are equivalent to the SI units for acceleration, ms^{-2} . Hence, the gradient of the graph represents the acceleration on the Moon. Thus, the experimental results indicate that the gravitational acceleration on the moon is 3.33 \ ms^{-2} . Part (b): The experiment was not accurate. The experimental value for the gravitational acceleration on the moon was 3.33 \ ms^{-2} , while the true value is 1.62 \ ms^{-2} . This means that the experimental error in the investigation is equal to: \begin{aligned} error \ \% &= \frac{ | experimental - true | }{ true} \times 100 \\\\ &= \frac{|1.62 - 3.33|}{1.62} \times 100 \\\\ &= 106 \ \% \end{aligned} This error value is extremely large and thus the experiment is highly inaccurate. Back to Question 10 |
Access over 500+ HSC Physics Module 5 Exam-Style Questions
Test your understanding of any HSC Physics Module 5 Advanced Mechanics concepts with Learnable’s customisable quizzes. Instant feedback provides immediate adjustments on your misconceptions. Try Learnable for free now.

Written by DJ Kim
DJ is the founder of Learnable and has a passionate interest in education and technology. He is also the author of Physics resources on Learnable.
Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.









