Test your exam readiness for HSC Physics Module 8
Module 8 ‘From The Universe to the Atom’ is the most conceptually challenging topic in HSC Physics. It explores the development of the atomic model and the origins of the universe.
A large number of students lose marks from Module 8 long-response questions because their written responses lack sufficient details.
In this article, we reveal:
- 17 commonly asked question types from the HSC Physics Module 8 Syllabus
- 10 exam long-response questions you are likely to be asked in your trial or HSC exam for Module 8 ‘From The Universe to The Atom’. Detailed solutions are included.
What are commonly asked exam question types in HSC Physics Module 8?
17 Commonly asked question types from the HSC Physics Module 8 Syllabus are listed below:
| NESA Content Block | Question Type |
| Origins of the Elements | - Describing the processes that led to the transformation of radiation into matter that followed the ‘Big Bang’.
- Discussing the evidence that led to the discovery of the expansion of the Universe by Hubble.
- Analysing the key features of stellar spectra and describing how these are used to classify stars.
- Using the Hertzsprung-Russell diagram to determine the following about a star:
- characteristics and evolutionary stage
- surface temperature
- colour
- luminosity
- Identifying and discussing the types of nucleosynthesis reactions involved in Main Sequence and Post-Main Sequence stars
|
| Structure of the Atom | - Assessing the experimental evidence supporting the existence and properties of the electron
- Assessing the experimental evidence supporting the nuclear model of the atom
|
| Quantum Mechanical Nature of the Atom | - Assessing the limitations of the Rutherford and Bohr atomic models.
- Examining the Balmer series in hydrogen quantitatively using the Rydberg equation.
- Discussing de Broglie’s matter waves and the experimental evidence that developed the formula \lambda=\frac{h}{mv}
- Analysing the contribution of Schrödinger to the current model of the atom
|
| Properties of the Nucleus | - Analysing the spontaneous decay of unstable nuclei, and the properties of the alpha, beta and gamma radiation emitted
- Making quantitative predictions about the activity or amount of a radioactive sample
- Explaining the process of nuclear fission, including the concepts of controlled and uncontrolled chain reactions, and account for the release of energy in the process
- Analysing relationships that represent conservation of mass-energy in spontaneous and artificial nuclear transmutations, including alpha decay, beta decay, nuclear fission and nuclear fusion
- Accounting for the release of energy in the process of nuclear fusion.
- Predicting quantitatively the energy released in nuclear decays or transmutations, including nuclear fission and nuclear fusion.
|
10 Must Know Questions for HSC Physics Module 8
Question 1 (5 marks)
Bohr’s atomic model is known as the first quantum model of the atom.
| (a) | Explain why the spectroscope was important in the development of the Bohr model of the atom. | 3 |
| (b) | Assess the limitations of the Bohr atomic model. | 2 |
See Question 1 Solution
Question 2 (2 marks)
Describe Schrödinger’s contributions to the quantum model of the atom.
See Question 2 Solution
Question 3 (6 marks)
The mass of a helium atom has been found to be 4.00389 \ u . The exact masses of proton, neutron and electrons in unified mass units are:
- m_{proton} = 1.007276 \ u
- m_{neutron} = 1.008664 \ u
- m_{electron} = 0.0005486 \ u
| (a) | Calculate the binding energy of the helium nucleus. | 3 |
| (b) | Using the law of conservation of mass-energy, explain why the mass of the nucleons inside the helium nucleus differs from their rest mass m_0 . | 3 |
See Question 3 Solution
Question 4 (5 marks)
The first atomic weapons were based on the uncontrolled fission of uranium (and plutonium). An example of a uranium fission reaction is shown below:
^1_0n + \ ^{235}_{92}U \rarr \ ^{141}_{56}Ba + \ ^{92}_{26}Kr + 3\big( ^1_0n \big)
The table below provides the mass of each particle within the reaction:
| Particle | Mass (amu) |
| ^{235} _{92} U | 235.0439299 |
| ^{92} _{26} Kr | 140.9144 |
| ^{141} _{56} Ba | 91.92617 |
| ^{1} _{0} n | 1.00867 |
| (a) | Explain what is meant by an uncontrolled fission chain reaction. | 2 |
| (b) | Use the information in the table to calculate the energy (in Joules) released by the reaction. | 3 |
See Question 4 Solution
Question 5 (5 marks)
According the Standard Model of Matter, all the particles in the universe can be grouped into just three “families” of elementary particles.
| (a) | State the three families of elementary particles in the standard model. | 1 |
| (b) | Outline the composition of the He-2 nucleus in terms of fundamental particles. | 2 |
| (c) | He-2 is an unstable isotope of helium. Its nucleus undergoes a positron decay. Write the nuclear reaction and hence state the force carrier particle responsible for the decay of a helium-2 nucleus. | 2 |
See Question 5 Solution
Question 6 (6 marks)
Particle accelerators are devices that accelerate particles to high velocities and energies. They are used to discover, investigate and understand the fundamental particles and physical laws that govern matter, energy and spacetime.
| (a) | Compare the operating principles of a cyclotron and synchrotron. | 2 |
| (b) | Describe how the key features and components of the standard model of matter have been developed using accelerators as a probe. | 4 |
See Question 6 Solution
Question 7 (6 marks)
A sketch of a Hertzsprung-Russell diagram is shown below.
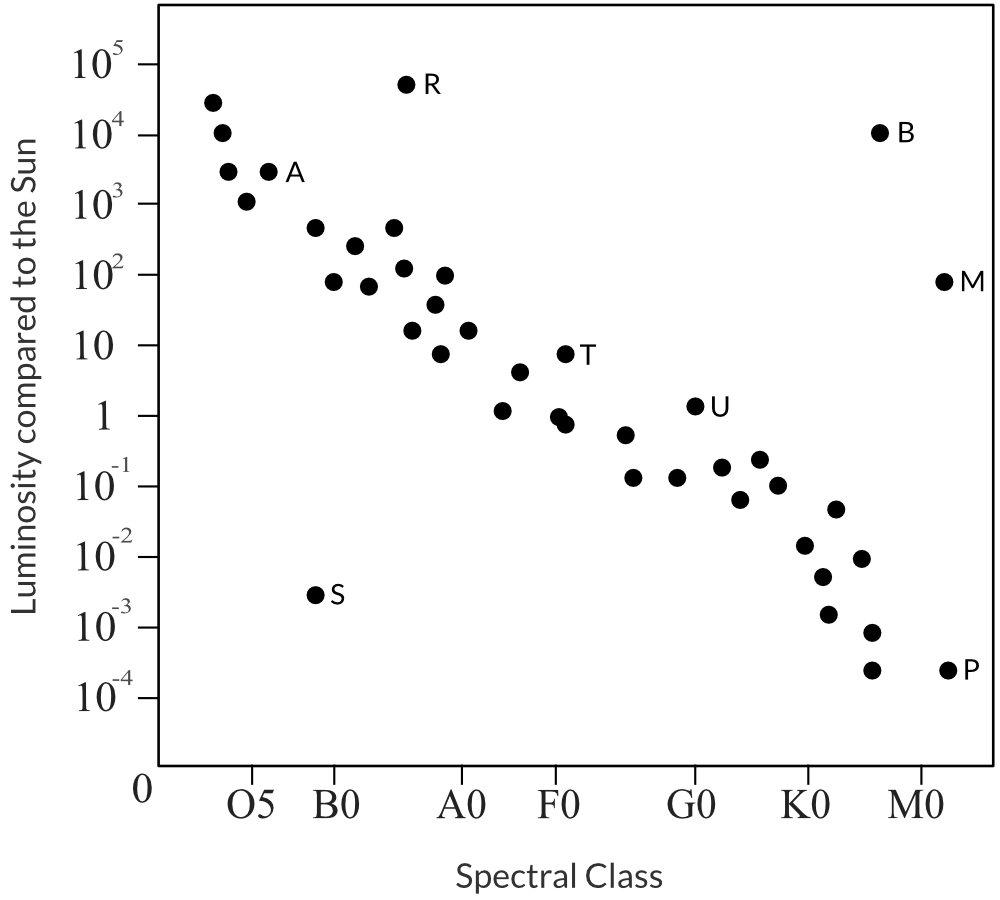
| (a) | Identify the stars that will evolve into a white dwarf. Provide a reason. | 2 |
| (b) | Outline the TWO nuclear reactions that are occurring in star M. | 2 |
| (c) | Explain the effect of the main sequence star’s mass on their life span. | 2 |
See Question 7 Solution
Question 8 (5 marks)
Energy can be produced in the cores of main sequence stars by two different nuclear processes.
| (a) | Identify the two nuclear processes. | 1 |
| (b) | Describe ONE similarity and ONE difference between these two processes. | 2 |
| (c) | Explain which feature of a star determines which of the two processes will be predominant in that star. | 2 |
See Question 8 Solution
Question 9 (2 marks)
What is the origin of the Cosmic Microwave Background radiation and why is the wavelength of the radiation in the microwave part of the spectrum?
See Question 9 Solution
Question 10 (6 marks)
Hubble’s Law states that the velocity of a galactic object relative to Earth is proportional to its distance from Earth:
v = H_0 d
| (a) | Outline the significance of Hubble’s Law. | 1 |
| (b) | Explain how Hubble used cosmic redshift observations and Cepheid variable stars to support Friedmann’s prediction of an expanding Universe. | 5 |
See Question 10 Solution
Solutions to HSC Physics Module 8 Questions
| Question | Solution |
| 1 | Part (a): For explain questions, students should use the CEO Framework (Cause, Effect, Outcome) to provide a logical and sequential response. The spectroscope allowed scientists to identify the characteristic spectral lines of different elements, including hydrogen. The Rutherford model of the atom had no electronic structure and was unable to explain the existence of atomic spectra. These spectral lines caused Bohr to hypothesise the existence of stable and fixed orbits for electrons, since the specific wavelengths of the lines suggested that there were fixed gaps between the available atomic electron energy levels. Without the spectroscope Bohr would not have made this hypothesis and would not have developed his model of the atom. Part (b): For assess questions, students should consider pros and cons and make a judgement. The Bohr atomic model was successful only in predicting spectral line wavelengths, and only of single electron species (e.g. \textrm H, \textrm H\textrm e^+ ). It was unable to explain the spectra of atoms larger than hydrogen, the relative intensities of spectral lines, Zeeman splitting or hyperfine splitting. This is due to Bohr’s model, with only one quantum number n , being an incomplete model of the atom. Back to Question 1 |
| 2 | Schrödinger developed the wave function model of the electron, treating the electron as a three dimensional standing wave. This model leads to the first three of four quantum numbers, n, l, m_l , required to explain how electrons exist in atoms. Back to Question 2 |
| 3 | Part (a): Step 1: Calculate the sum of masses of the components. - m_{protons} = 2 \times 1.007276 = 2.014552 \ u
- m_{neutrons} = 2 \times 1.008664 = 2.017328 \ u
- m_{electrons} = 2 \times 0.0005486 = 0.0010972 \ u
Step 2: Calculate the mass defect by subtracting the mass of the nucleus from the masses of the constituents. \begin{aligned} \Delta m &= m_{components} - m_{helium} \\\\ &= (2.014552 + 2.017328 + 0.0010972) - 4.00389 \\\\ &= 0.0290872 \ u \end{aligned} Step 3: Using the result obtained in Step 2, calculate the binding energy of the helium nucleus. \begin{aligned} E &= 0.0290872 \times 931.5 \\\\ &= 27.0947 \ MeV \end{aligned} Part (b): The Law of Conservation of mass-energy extends Einstein’s theory of mass-energy equivalence. Since mass is a type of energy, it can be transformed into other forms of energy. This means that mass on its own is no longer required to be conserved. When an atom is formed, the constituent nucleons each lose a small amount of mass. Consequently, the mass of the nucleus is less than the summed mass of the individual, separate particles. By the Law of Conservation of mass-energy, the “lost” mass is conserved and is converted into energy according to E = \Delta mc^2 . Separating the nucleus into individual nucleons requires work, which corresponds to the binding energy of the nucleus. Back to Question 3 |
| 4 | Part (a): An uncontrolled fission chain reaction refers to a fission chain reaction where the reproduction constant K is greater than 1. This means that more than one neutron from each fission reaction will go on to trigger another fission reaction. Since each fission leads to more than one subsequent fission the reaction rate will increase exponentially, resulting in an uncontrolled fission chain reaction. Part (b): Step 1: Calculate the mass defect of the reaction. \begin{aligned} \Delta m &= m_{reactants} - m_{products} \\\\ &= (235.0439299 + 1.00867) - (140.9144 + 91.92617 + 3 \times 1.00867) \\\\ &= 0.1860199 \ u \end{aligned} Step 2: Apply E = m \times 931.5 to calculate the energy released in the reaction. \begin{aligned} E &= 0.1860199 \times 931.5 \\\\ &= 173.2775 \ MeV \end{aligned} |
| 5 | Part (a): The three families of elementary particles in the standard model of matter are: Quarks, Leptons and Bosons. Part (b): A Helium-2 nucleus consists of 2 protons and no neutrons. Each proton consists of two up quarks and one down quark. Part (c): A Helium-2 nucleus undergoes a positron decay. This turns the isotope into deuterium. The nuclear reaction for this decay is expressed as: ^2_2He \rarr \ ^2_1D + \ ^0_1e + \ \nu_e + energy The force carrier particle responsible for positron decay is the W Boson. Back to Question 5 |
| 6 | Part (a): A cyclotron is a circular disk-shaped accelerator that uses electric fields to accelerate charged particles, and confines them in a circular path of increasing radius (an outward spiral) with the use of a constant magnitude magnetic field. As a charged particle gains energy, the radius of its orbit increases, and it spirals out to the limit of the magnetic pole area. In comparison, a synchrotron is a circular ring-shaped accelerator that uses electric fields to accelerate charged particles, and confines them in a circular path of fixed radius by synchronising the magnetic field strength with the energy of the accelerated particles. The magnetic field strength is increased as the energy of the particle is increased. The particles to travel in a circular loop, rather than a spiral. Part (b): The Standard Model of Matter describes the elementary particles of matter, and the forces by which they interact (excluding gravity). According to the Standard Model, all particles in the Universe can be grouped into three families of elementary particles; Quarks, Leptons and Bosons. The first subatomic particle (an electron) was discovered using the an accelerator known as a cathode ray tube. As electrons are elementary particles, this was the discovery of the first particle in the Standard Model. Rutherford additionally used alpha sources (natural accelerators) to bombard different materials, leading to the discoveries of nuclei, the proton and the neutron. This was the limit of what natural accelerators could identify due to the limited energies of the alpha particles. In 1969 the Stanford Linear Accelerator achieved much higher energies than natural accelerators and discovered that protons were not fundamental, but were made of smaller particles. This saw the discovery of quarks, which led to a huge advancement in the understanding of matter and the development of the Standard Model. The development of synchrotrons allowed even greater particle collision energies, producing particles that could not be identified under normal conditions. This played a crucial role in the discovery and understanding of the rest of the particles described in the Standard Model. This culminated in the Large Hadron Collider’s discovery of the Higgs Boson in 2012, which is the final particle to be verified in the Standard Model. Back to Question 6 |
| 7 | Part (a): Stars T, U and P will evolve into White Dwarfs. Main Sequence stars will evolve into White Dwarfs if their mass is between 0.1 and 8 solar masses. This corresponds to spectral classes from M to B. From the diagram stars T, U and P all satisfy this condition. Part (b): Star M is a red giant. This can be identified by analysing the HR diagram. Red giants undergo two nuclear reactions: - Hydrogen shell burning,
- Core helium fusion.
Hydrogen shell burning involves the fusion of hydrogen into helium in a shell around the star’s helium core. The helium produced sink into the core. Core helium fusion involves the fusion of helium into heavier nuclei within the star’s core. This occurs within the star’s hydrogen-burning shell. Part (c): Higher mass stars live shorter lifetimes, despite having more fuel for fusion. The time taken to consume core and shell fuel supplies (e.g. hydrogen) is inversely proportional to the mass, since higher mass results in stronger gravitational forces. This in turn leads to substantially higher fusion rates, and the larger fuel supplies are consumed in a shorter time. Back to Question 7 |
| 8 | Part (a): The two nuclear processes are: - The proton-proton chain, and
- The CNO cycle.
Part (b): Similarity: - Four hydrogen nuclei are progressively fused into a single helium-4 nucleus.
Difference: - In the CNO cycle carbon-12 nuclei act as nuclear catalysts to facilitate the reaction (and are ultimately not changed by it). In the proton-proton chain, there is no nuclear catalyst.
Part (c): The mass of a main sequence star will determine which of the two nuclear processes will dominate in the star. In higher mass stars, the CNO cycle will dominate. This is due to: - Higher mass stars have higher core temperatures. This allows the CNO cycle to occur.
- Higher mass stars have more carbon-12 readily available in the core. Lower mass stars have insufficient amounts of Carbon-12.
Back to Question 8 |
| 9 | Before atoms formed the Universe consisted of free nuclei and electrons. These free charged particles constantly absorbed and emitted (i.e. scattered) light. Once the Universe expanded and cooled sufficiently electrons combined with nuclei to form neutral atoms, which cause dramatically less scattering of light. The light that was suddenly free to travel the Universe has been propagating ever since, and due to cosmic expansion has been redshifted into microwave wavelengths. Back to Question 9 |
| 10 | Part (a): Hubble’s Law is observational proof of the expansion of space. Objects at larger distances are seen to recede at higher velocities, due to the larger amount of expanding space between them and Earth. This is the observation expected in an expanding Universe, hence this evidence directly supports the Big Bang theory. Part (b): Cepheid variable stars were seen to pulsate in intensity or brightness B with consistent period T . By using parallax to measure the distance r to nearby Cepheids, their luminosity L could be calculated from the inverse square law, B = \frac{L}{4\pi r^2} . It was found that there was a clear proportionality between the luminosity of a Cepheid and its period of pulsation, establishing a period-luminosity relationship. This information was then used with observations of very distant Cepheids that were too far away for parallax to provide distance. Their observed periods of pulsation were used with the period-luminosity relationship to determine their luminosities by the relationship. The observed intensities and inferred luminosities then allowed their distances to be found. Meanwhile, Hubble had observations of the visible spectra of the same distant galaxies in which Cepheids were observed. The spectra of those galaxies exhibited redshifted spectral lines, indicating they had velocities away from Earth. The amount of spectral line redshift is proportional to the velocity. The velocity of the light source (the galaxy) can be determined from the Doppler equation. f' = f \frac{ v_{wave} + v_{observer} }{ v_{wave} - v_{source} } Hubble then combined the velocities from spectral redshifts with the distances from Cepheid variable observations and discovered that the more distant galaxies had higher recession velocities. The recession velocity was directly proportional to the distance, v = H_0 d , now known as Hubble’s Law. This was direct evidence of cosmic expansion and thus supported Friedmann’s prediction of an expanding Universe. Back to Question 10 |
Access our library of HSC Physics Module 8 Exam Questions
Test your understanding of any HSC Physics Module 8 concepts in just 10 minutes with Learnable’s customisable quizzes with over 500+ questions for each module. Instant feedback provides immediate adjustments on your misconceptions. Try Learnable for free now.

Written by DJ Kim
DJ is the founder of Learnable and has a passionate interest in education and technology. He is also the author of Physics resources on Learnable.
Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.

