HSC Physics Module 7 Practice Questions with Solutions
Test your exam readiness with these 10 Must Know Physics Module 7 questions
HSC Physics Module 7 The Nature of Light is considered by many students as the most interesting module in the Physics course. It explores the development of quantum mechanics and the “strangeness” of the Special Theory of Relativity.
Students find Special Relativity fascinating but difficult to comprehend.
In this article, we reveal:
- 11 important question types from the HSC Physics Module 7 Syllabus
- 10 Must Know questions to ace your next HSC Physics Module 7 Exam
What type of questions are commonly asked in HSC Physics Module 7?
11 commonly asked question types from the HSC Physics Module 7 Syllabus are listed below:
| NESA Content Block | Question Type |
| Electromagnetic Spectrum |
|
| Light: Wave Model |
|
| Light: Quantum Model |
|
| Light and Special Relativity |
|
Source: NESA website
10 Must Know Questions for HSC Physics Module 7
Question 1 (5 marks)
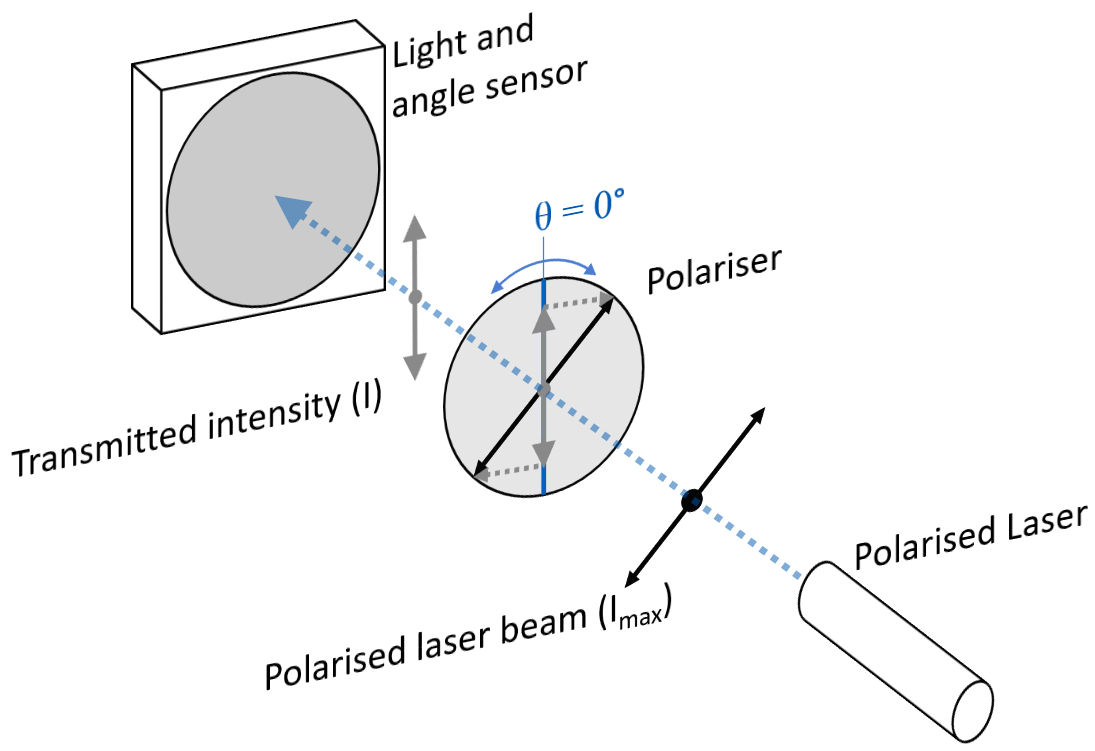
A student conducts an experiment to investigate Malus’ law. Their light source is a laser that emits light polarised at an unknown angle. To conduct this experiment the student uses a detector with a light sensor and angle sensor.
The light sensor measures the intensity I of incident light. In front of the light sensor there is a polariser, which can be rotated or removed. The angle sensor measures the angle \theta of the polariser.
A schematic diagram of the apparatus is shown below, with the polariser currently in place and vertical at \theta = 0 \degree .
The student records the following data from conducting their experiment:
| Angle Sensor Reading (degrees) | Light Sensor Reading (Wm ^{-2}) | Angle \theta between laser polarisation and polariser (degrees) |
| 0 | 3.75 | |
| 10 | 4.41 | |
| 30 | 5.00 | |
| 40 | 4.85 | |
| 70 | 2.94 | |
| 90 | 1.25 |
| (a) | Describe a procedure that would be suitable to investigate Malus’ Law using this equipment. | 2 |
| (b) | The intensity of the laser is 5.00 \ Wm^{-2} . Complete the third column of the table above by finding the angle between the laser polarisation and the polariser. | 1 |
| (c) | Explain why this experiment verifies Malus’ Law. | 2 |
Question 2 (4 marks)
An experimental setup to demonstrate Young’s double slit experiment is shown below.
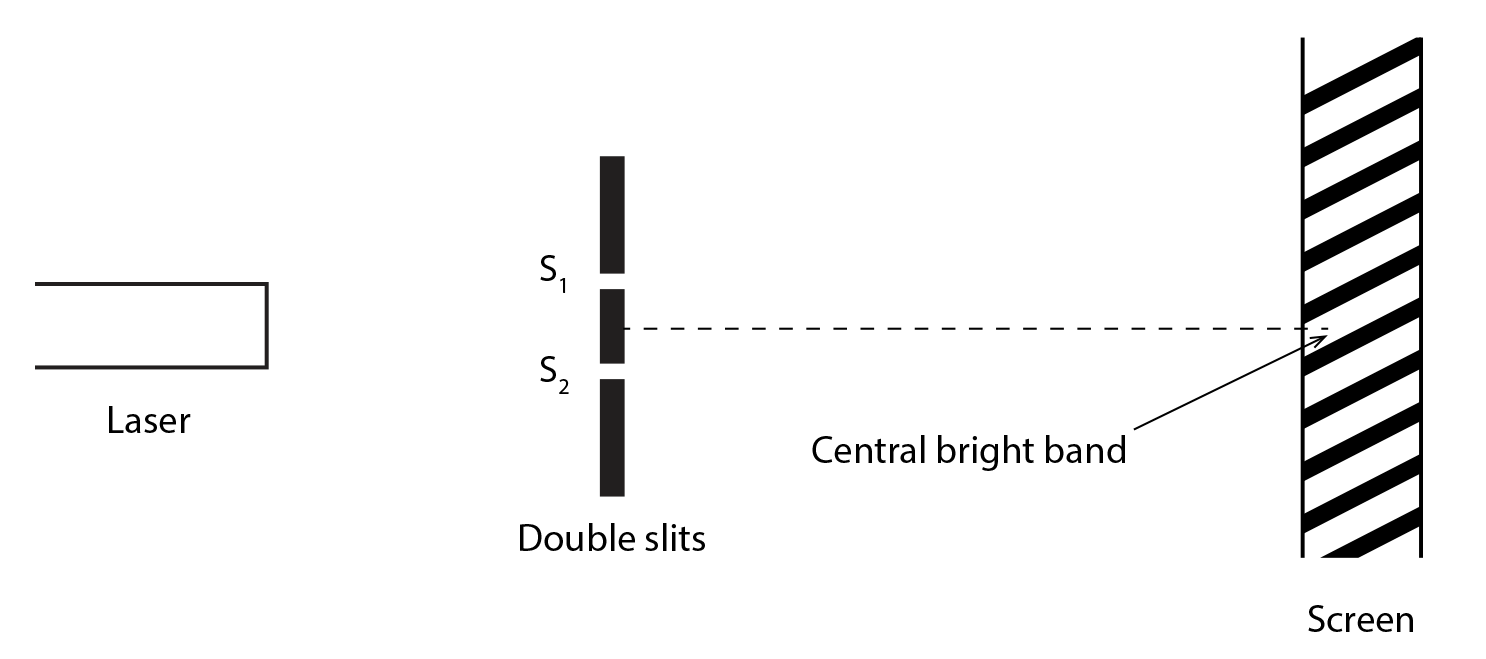
Monochromatic light is passed through a double slit and the interference pattern is projected onto a screen. The distance between the central bright fringe and the bright fringes adjacent to it is 10 \ cm .
| (a) | The student makes an adjustment that resulted in the new distance between the central bright fringe and the adjacent bright fringes increasing to 30 cm. Outline TWO possible changes the student could have made. | 2 |
| (b) | At the time Young’s double-slit experiment was conducted, there were two competing models of the nature of light. Explain how Young’s experiment supported one of the models. | 2 |
Question 3 (3 marks)
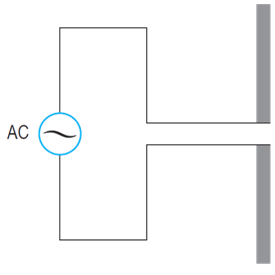
The diagram below shows an AC voltage connected to the wires of an antenna. This is a common technique for producing radio waves.
| (a) | Explain how the apparatus shown produces radio waves. | 2 |
| (b) | With reference to a classical theory of light, outline Maxwell’s contribution to our understanding of light that was supported by the discovery of radio waves. | 3 |
Question 4 (7 marks)
A plot of some experimental blackbody radiation spectra at different temperatures is shown in the diagram below, together with a spectrum predicted by classical theory.
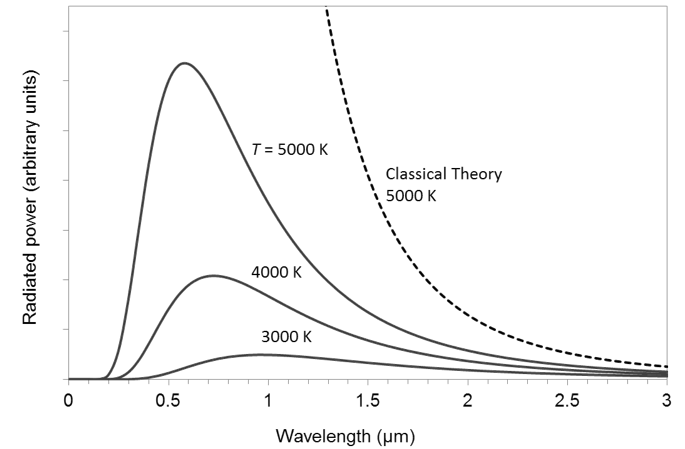
| (a) | Explain how Planck accounted for the discrepancy between the experimental results and the predictions of classical theory. | 3 |
| (b) | Describe results of two experiments that support Planck’s hypothesis regarding black body radiation. | 3 |
| (c) | Using Planck’s energy equation, determine the energy (in joules) of a released quantum of red light if it has a wavelength of 700 \ nm . Express your answer to three significant figures. | 1 |
Question 5 (3 marks)
Spectroscopy can be used to determine a large amount of information about objects in the galaxy. The following spectrum of a star was recorded.
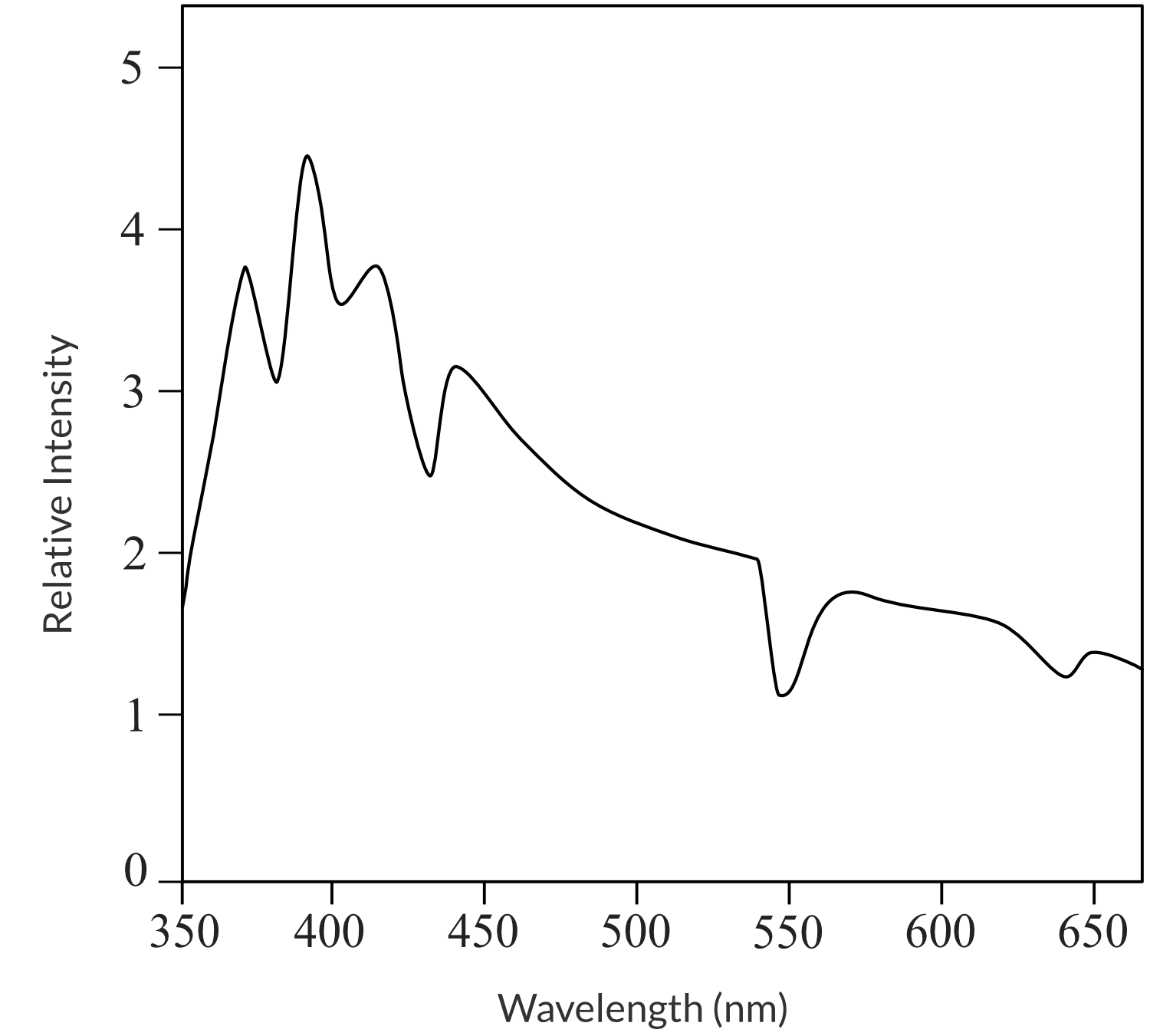
Explain what information about the star can be determined from this spectrum.
Question 6 (6 marks)
Light is incident on a Zirconium surface in a vacuum. The graph below shows the variation of the stopping voltage V_{s} of the electrons emitted from the surface with the frequency f of the incident light.
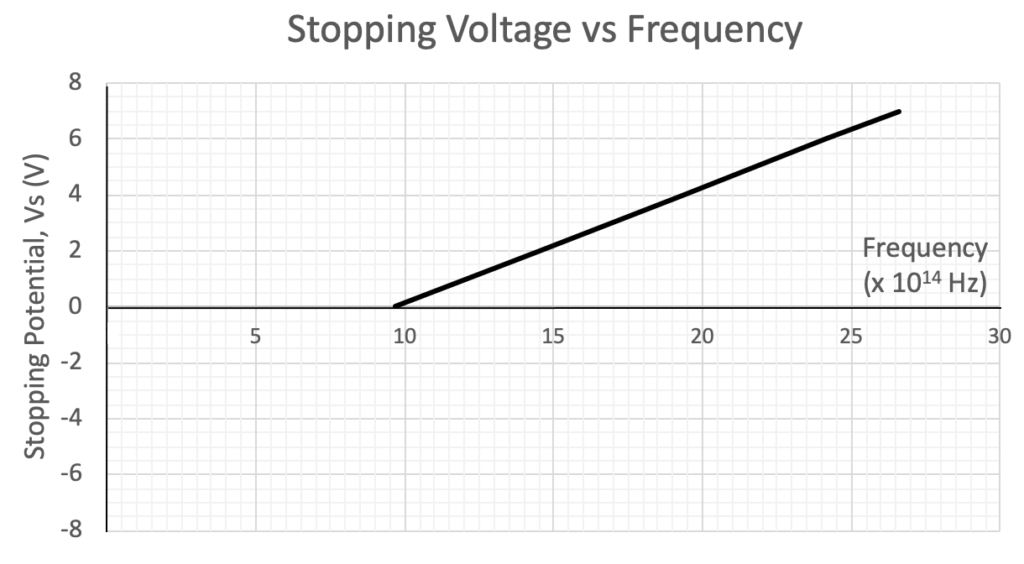
| (a) | From the graph, determine the work function of Zirconium. | 2 |
| (b) | Explain how the graph of stopping voltage variation with incident light frequency provides evidence supporting the particle model of light. | 3 |
Question 7 (3 marks)
The principle of relativity was proposed by Galileo Galilei in 1632.
| (a) | State Galileo’s principle of relativity. | 1 |
| (b) | Describe the consequences of Galileo’s principle of relativity on observers in both inertial and non-inertial frames of reference. | 2 |
Question 8 (6 marks)
A spacecraft leaves Earth at a speed of 0.80 \ c as measured by an observer on Earth. It heads towards, and continues beyond, a distant planet in the star system Gliese 3325. The planet is 30 light years (ly) away from Earth as measured by an observer on Earth.

When the spacecraft leaves Earth, Emmet, one of the astronauts in the spacecraft, is 20 years old.
| (a) | Calculate the time taken for the journey to the planet as measured by an observer on Earth. | 2 |
| (b) | Calculate the distance between the Earth and the planet, as measured by Emmet. | 2 |
| (c) | As the spacecraft goes past the planet, Emmet sends a radio signal to Earth. Calculate, as measured by the spacecraft observers, the time it takes for the signal to arrive at Earth. | 2 |
Question 9 (5 marks)
A deuteron (which consists of 1 proton and 1 neutron) is accelerated from rest to a speed of 0.8 \ c in a particle accelerator.
- Mass of a proton: 1.673 \times 10^{-27} \ kg
- Mass of a neutron: 1.675 \times 10^{-27} \ kg
| (a) | Calculate the accelerating potential V in volts required to achieve this velocity. | 3 |
| (b) | Calculate the work required to accelerate the deuteron from 0.8 \ c to 0.9 \ c . | 2 |
Question 10 (6 marks)
Around 1850 a French scientist Leon Foucault performed an experiment to determine whether light travels faster in air or in water. His experimental setup is shown below.
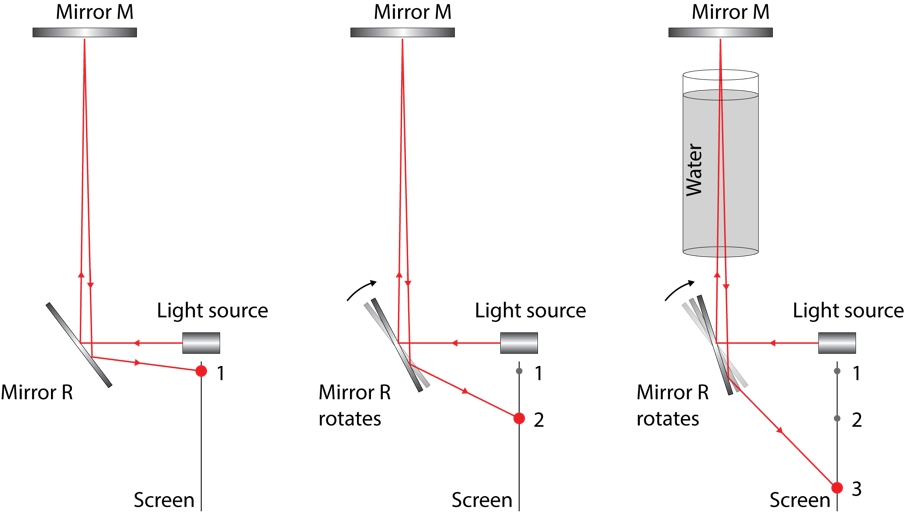
In Foucault’s experiment a beam of light is reflected off mirror R to mirror M, back to mirror R, and then to position 1 on a screen, as shown in the left diagram.
Mirror R is then spun clockwise at a high rate, as shown in the middle diagram. Due to the rotation of mirror R during the flight time of the beam of light, the returning beam is reflected to a displaced position on the screen, position 2.
In the third phase of the experiment a 3 m long tube of water is placed between mirrors M and R, in the path of the beam of light, as shown in the diagram on the right.
| (a) | Outline the results of his experiment. | 2 |
| (b) | Which early theories of light did the results of this experiment support or refute? Justify your answer by outlining each of the theories. | 4 |
Solutions to HSC Physics Module 7 Practice Questions
Detailed, step-by-step solutions to the Module 5 Advanced Mechanics questions are provided below.
Marking practice exams is just as important as answering the questions
Question 1 Solution
Part (a):
- Direct the laser beam into the detector. Measure the laser intensity in the absence of the polariser to obtain the control variable I_{max} .
- Put the polariser in place and rotate it to specific angles, recording the measured laser intensity for each angle of the polariser. Use at least 5 different values of \theta .
- Analyse the data, specifically by plotting a graph of \frac{I}{I_{max}} vs cos^2 \theta .
- Malus’ Law is I = I_{max} cos^2 \theta , which will be verified if the graph produced in Step 3 exhibits a gradient of 1.
Part (b):
Given the laser intensity is I_{max} = 5.00 \ Wm^{-2} , the ratio \frac{I}{I_{max}} can be found from the intensity measurements recorded in the experiment.
Assuming Malus’ Law, \theta can be found as follows:
\begin{aligned} \dfrac{I}{I_{max}} &= \cos^2 \theta \\\\ \cos \theta &= \sqrt{\dfrac{I}{I_{max}}} \\\\ \therefore \theta &= \cos^{-1} \bigg(\sqrt{\dfrac{I}{I_{max}}}\bigg) \end{aligned}
Calculating (\theta) for each measured intensity yields:
| Angle \theta between laser polarisation and polariser (degrees) |
| 30 |
| 20 |
| 0 |
| 10 |
| 40 |
| 60 |
Part (c):
Step 1: Plot a graph of \dfrac{I}{I_{max}} \ vs \ \cos^2 \theta . Draw a line of best fit through your data.
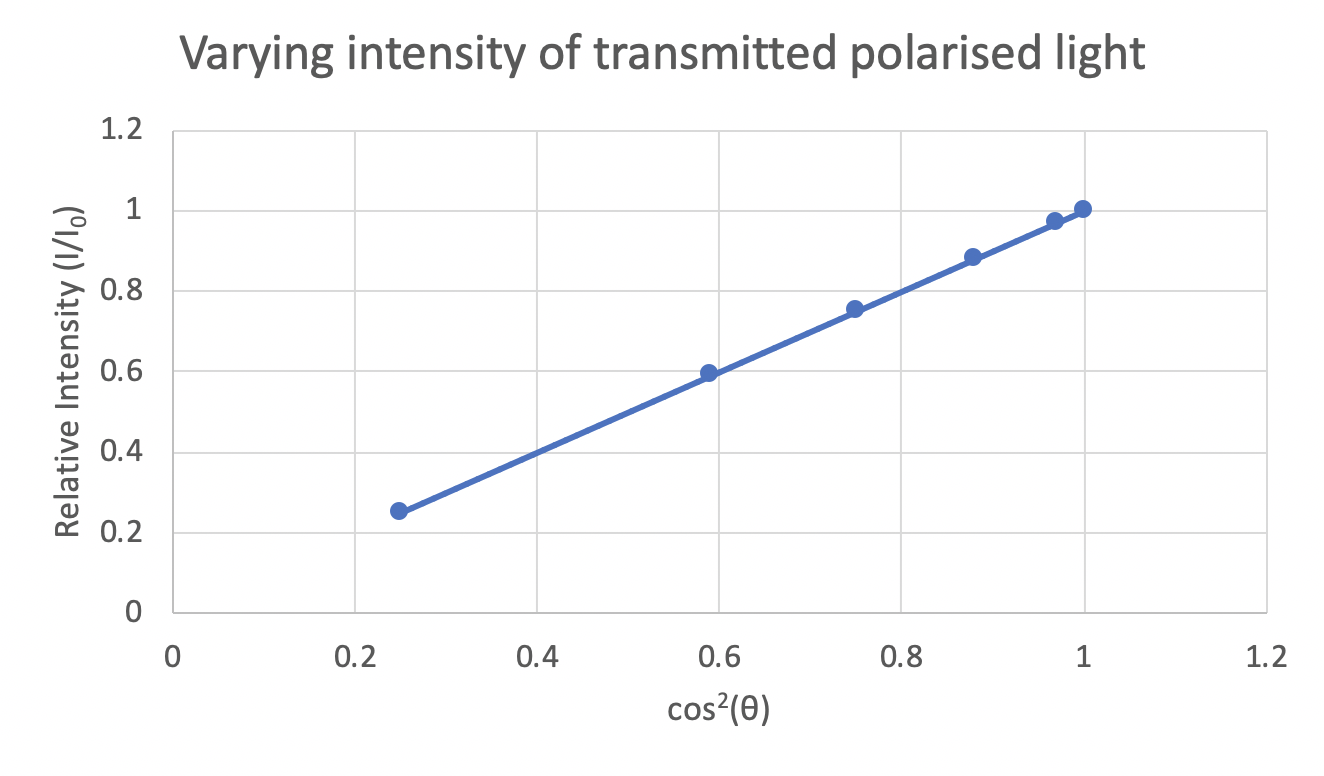
Step 2: Calculate the gradient of the line of best fit.
The gradient of the line of best fit is calculated from m = \frac{rise}{run} :
\begin{aligned} m &= \dfrac{rise}{run} \\\\ &= \dfrac{0.6-0.4}{0.6-0.4} \\\\ &= \dfrac{0.2}{0.2} \\\\ &= 1 \end{aligned}
Therefore, y = x and hence \dfrac{I}{I_{max}} = \cos^2 \theta . Rearranging this equation, I = I_{max} \cos^2 \theta . This is Malus’ Law, which is thus verified by this experiment.
Question 2 Solution
Part (a):
For the bright fringe adjacent to the central bright fringe, m = 1 , in the relationship:
d\sin \theta = m \lambda
For a small \theta , \sin \theta = \tan \theta= \frac{h}{L}:
\begin{aligned}\therefore \frac{dh}{L} &= \lambda \\\\ h &= \frac{ \lambda L}{d} \end{aligned}
The separation on the screen of the central bright fringe and the adjacent bright fringes can be increased from 10 \ cm to 30 \ cm by:
- Moving the screen to three times the initial distance, 3L .
- Increasing the wavelength of light to three times the initial wavelength, 3\lambda .
- Decreasing the slit spacing to one third of the initial spacing, \frac{1}{3}d .
Note that there are THREE possible changes that could be made, of which the question requires TWO, so choose two from the above list.
Part (b):
Young’s double slit experiment demonstrated the occurrence of interference effects with light, which produced the pattern of bright and dark fringes on the screen. The wave model of light was able to explain the interference effect, while the particle model could not provide an explanation. Hence, Young’s double slit experiment supported the wave model of light.
Question 3 Solution
Part (a):
Radio waves are electromagnetic waves. The AC powered antenna setup includes a dipole – the two separate metal rods. The application of AC causes charge to oscillate between the two rods of the dipole, resulting in changing electric and magnetic fields around the dipole antenna.
These changes in electric and magnetic field propagate sideways away from the antenna at the speed of light, as a transverse wave. This is an electromagnetic wave. The frequency of the wave is determined by the frequency of AC, so radio frequency AC produces radio waves.
Part (b):
Maxwell unified known, empirical laws of electricity and magnetism into the theory of electromagnetism, as expressed by Maxwell’s equations, which describe all electromagnetic phenomena. Maxwell’s equations can be combined to derive the wave equation, which predicts electromagnetic waves travel at a speed of v = 3 \times 10^8 \ ms^{-1} in a vacuum. This is the known speed of light.
The theory also predicts that electromagnetic waves are transverse. The agreement between the speed of the hypothesised electromagnetic waves and the known speed of light led Maxwell to propose that light must be an electromagnetic oscillation, i.e. an electromagnetic wave.
Question 4 Solution
Part (a):
When approaching questions about Planck’s explanation of black body radiation, students should be aware of the following context:
Classical theory predicts that atoms can exist at any energy and oscillate at any frequency, and that there is no preferred frequency for emitted radiation. Hence all frequencies are emitted equally. Given c = fλ, hence λ = c/f, therefore shorter wavelengths should dominate at any temperature.
Planck proposed that the intensity and hence energy of radiation emitted by a black body could only be increased by fixed amounts proportional to the frequency of radiation, given by E = hf . This required atoms to have discrete (or quantised) energy levels, and hence the atomic energy changes associated with radiation emission must be discrete changes. (1 mark)
At a given temperature one such discrete energy change would be most probable, hence occur most often, giving rise to the peak wavelength in the spectrum – a wavelength of light emitted more than any other and thus having the highest intensity. (1 mark)
Furthermore, atoms lack sufficiently large discrete energy changes to able to produce high frequency (short wavelength) radiation such as X-rays and gamma rays. Consequently, these wavelengths are not observed at any temperature. (1 mark)
Part (b):
Classical theory could not explain the photoelectric effect, while the concept of quantised light energy (photons with energy E = hf ) was able to fully explain the phenomenon. The maximum kinetic energy of the ejected electrons was found to be K_{max} = hf - \phi , where the photon energy hf must exceed the work function \phi of the metal, else electrons are not ejected.
Classical theory could also not explain the emission line spectra from gases in discharge tubes. The specific wavelengths of emission (while no other wavelengths were emitted) constitute direct evidence of discrete (i.e. quantised) energy levels in atoms.
Part (c):
Planck’s energy equation is E = hf . This can be re-written as E = \dfrac{hc}{\lambda} using the equation v = c = f \lambda .
By substituting the value for wavelength into this equation, we can calculate the energy of a quantum of red light:
\begin{aligned} E &= \dfrac{hc}{\lambda} \\\\ &= \dfrac{ 6.626 \times 10^{-34} \times 3 \times 10^8 }{ 700 \times 10^{-9} } \\\\ &= 2.84 \times 10^{-19} \ J \ (3 \ s.f.) \end{aligned}
Question 5 Solution
The surface temperature T of the star can be determined from the peak wavelength \lambda_{max} of the black body spectrum by using Wien’s Law: \lambda_{max} = \frac{2.898 \times 10^{-3}}{T} .
The chemical composition of the stellar atmosphere is determined from the presence of spectral lines. Laboratory spectra of atoms/molecules can be used to identify those elements/compounds in the spectrum of the star. The strengths (depths) of the absorption lines are proportional to the concentrations of the atoms/molecules, indicating how much of each chemical is in the star’s atmosphere.
Students could also discuss information gained from the broadening of spectral lines:
The rotational velocity of the star can be determined from the extent of broadening of spectral lines (whole line) while density can be determined from the extent of pressure broadening (wings of line).
Question 6 Solution
Part (a):
The magnitude of the stopping voltage in volts is equal to the magnitude of the maximum kinetic energy in electron volts. Therefore, a graph of stopping voltage vs frequency can be interpreted as a graph of maximum kinetic energy vs frequency. Hence, the y-intercept of the graph represents the work function \phi , in electron volts.
By extrapolating the graph back to the y-axis, the work function of Zirconium is found to be 4 \ eV .
Part (b):
From the graph, a relationship between maximum kinetic energy and frequency of incident light can be obtained.
The gradient of the graph is equal to Planck’s constant h .
\begin{aligned} y &= mx + c \\ K_{max}& =gradient \times f - \phi \\ K_{max}& =hf - \phi \end{aligned}
From the photoelectric effect equation, we can infer:
- the maximum kinetic energy K_{max} of ejected photoelectrons is directly proportional to the frequency f of light.
- the energy absorbed by an electron is equal to the energy carried by a photon hf .
This supports the particle model of light, which stated that the energy of the photon is determined by its frequency by E = hf and there is a one-to-one interaction between an electron and a photon.
Question 7 Solution
Part (a):
Galileo’s principle of relativity states that the mechanical laws of physics are the same for every observer moving uniformly with constant speed in a straight line (i.e. for every observer in an inertial frame).
Part (b):
Galileo’s principle of relativity states that there is no physical way, from within an inertial frame, to differentiate between a body moving at a constant speed (one inertial frame of reference) and a body at rest (another inertial frame of reference). This means that constant motion cannot be detected in an inertial frame of reference.
However, acceleration can be detected in non-inertial frames of reference. This means that the principle of relativity holds true for any frames of reference that are not accelerating (i.e. inertial frames of reference).
Question 8 Solution
Part (a):
Using the formula, t = \frac{d}{v} , we can calculate the time taken for the journey to the planet.
t = \frac{30 \ \text{c years}}{0.80 \ c } = 37.5 \ years
1 light year can be written as 1 c year.
Part (b):
Using the formula for length contraction, we can calculate the distance between the Earth and the planet as measured by Emmet on the spacecraft:
\begin{aligned} l &= l_0 \times \sqrt{1-\frac{v^2}{c^2}} \\\\ &= 30 \times \sqrt{1-\frac{0.8c^2}{c^2}} \\\\ &= 30 \times \sqrt{1-0.64} \\\\ &= 18 \ light \ years \end{aligned}
Part (c):
Let the time taken for the signal to arrive at Earth be denoted by T . This means that the signal reaches Earth after travelling a distance of cT .
However, this distance is also equal to 18 light years (from part (b)) plus the distance travelled by the Earth in time T , i.e:
d = 18 \text{c years} + 0.80 cT
By rearranging this equation, we can calculate the time taken for the signal to arrive at earth:
\begin{aligned} cT &= 18c + 0.80 cT \\\\ \therefore 0.20 T &= 18 \ \text{c years} \\\\ T &= 90 \ years \end{aligned}
Question 9 Solution
Part (a):
\begin{aligned} E &= m_0 c^2 \\\\ &= (1.673 \times 10^{-27} + 1.675 \times 10^{-27})c^2 \\\\ &= 3.348 \times 10^{-27} \times (3 \times 10^8) ^2 \\\\ &= 3.0132 \times 10^{-10} \ J \end{aligned}
\begin{aligned} E_{0.8 \ c} &= m_v c^2 \\\\ &= \frac{ ( m_0 c^2 ) }{ \sqrt{ 1 - \frac{ v^2 }{ c^2 } } } \\\\ &= \frac{ ( 3.0132 \times 10^{-10} ) }{ \sqrt{ 1 - (0.8)^2 } } \\\\ &= 5.022 \times 10^{-10} \ J \end{aligned}
\begin{aligned} K &= m_{\nu} c^2 - m_0 c^2 \\ \Delta K&=qV \\ E_{0.8 \ c} - E_{rest}&= qV \\ V&= \frac{E_{0.8c} - E_{rest}}{q} \\ &=\frac{5.022 \times 10^{-10} -3.0132 \times 10^{-10}}{1.602 \times 10^{-19}} \\ &= 1.254 \ GV \end{aligned}
Part (b):
Step 1: Calculate the total energy of the deuteron when it is travelling at 0.9 \ c .
\begin{aligned} E_{0.9c} &= m_v c^2 \\\\ &= \frac{ ( m_0 c^2 ) }{ \sqrt{ 1 - \frac{ v^2 }{ c^2 } } } \\\\ &= \frac{ ( 3.0132 \times 10^{-10} ) }{ \sqrt{ 1 - (0.9)^2 } } \\\\ &= 6.912 \times 10^{-10} \ J \end{aligned}
Step 2: Calculate the work required to increase the energy of the deuteron from the previous value at v = 0.8 \ c to the new value at v = 0.9 \ c .
\begin{aligned} W &= E_{0.9 c} - E_{0.8 c} \\\\ &= 6.912 \times 10^{-10} - 5.022 \times 10^{-10} \\\\ &= 1.890 \times 10^{-10} \ J \end{aligned}
Question 10 Solution
Part (a):
Light travelling through only air reached the screen at position 2. Light travelling through air and the tube of water reached the screen at a more displaced position on the screen, position 3.
Part (b):
Foucault’s experimental results indicated that light travels slower in water than in air. The presence of the tube of water increased the flight time of the beam of light (by slowing the light down), which allowed the spinning mirror to rotate more and reflect the returning beam of light to a more displaced position on the screen.
At the time there were two major and competing models of light: Huygens’ wave model and Newton’s corpuscle model. For light entering a more dense medium:
- Huygens’ model predicted that waves of light will decrease in velocity.
- Newton’s model predicted that corpuscles of light will increase in velocity.
Hence Foucault’s result refuted Newton’s corpuscle model and supported Huygens’ wave model.
Access our library of HSC Physics Module 7 Exam Questions
Test your understanding of any HSC Physics Module 7 concepts in just 10 minutes with Learnable’s customisable quizzes with over 500+ questions for each module. Instant feedback provides immediate adjustments on your misconceptions. Try Learnable for free now.
Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.