In this article
HSC Physics Trial Papers | Free Mock Physics Practice Exam
Mock HSC Physics Trial Exam Paper
Looking for past trial exam papers for Physics?
This free Physics trial paper assesses your understanding of the following modules:
- Module 5: Advanced Mechanics
- Module 6: Electromagnetism
- Module 7: The Nature of Light
This Physics trial paper written for the new syllabus covers modules 5 – 7 as most schools do not include Module 8 in their Physics trial exam.
Advice for getting the most out of Mock HSC Physics Trial Exam Paper
It is recommended you complete
- Module 5-7 theory lessons and quizzes on the Year 12 Physics course on Learnable before attempting this exam to ensure you perform your best.
- Read the Exam skills including Common Mistakes & Misconceptions for each module
The most effective way to finalise your exam preparation for Physics is to attempt as many practice papers as possible under exam conditions.
Instructions for sitting the 2020 HSC Physics Trial Exam Paper
Please read and follow the instructions carefully to avoid any loss of marks:
- Working time is 3 hours.
- Attempt all questions.
- You must write in black pen. Do not write in pencil.
- You may only use a pencil for drawing diagrams and graphs.
- All necessary working should be shown in every question. Marks may be deducted for careless or badly arranged work.
- Set out all working for numerical questions and provide appropriate units.
- You may refer to a formulae sheet and data sheet.
- Calculators approved by NESA may be used.
Copyright
Copyright © 2024 Learnable Education. All rights reserved. No part of this material may be reproduced, stored in or introduced into a retrieval system or transmitted, in any form, or by any means (electronic, mechanical, photocopying, recording, or otherwise), without the prior permission of Learnable Education.
2024 HSC Physics Trial Exam Paper
Section I: Multiple Choice
In Section I of Mock Physics Trial Paper:
- There are 20 multiple choice questions.
- Each question is worth 1 mark.
- Allow 35 minutes for this section.
Question 1
A recently discovered planet has four times the mass and half the radius of Earth. What is the magnitude of the gravitational acceleration on the surface of the planet?
(A) 2 \ g
(B) 4 \ g
(C) 8 \ g
(D) 16 \ g
Question 2
A projectile is launched by a cannon as shown.
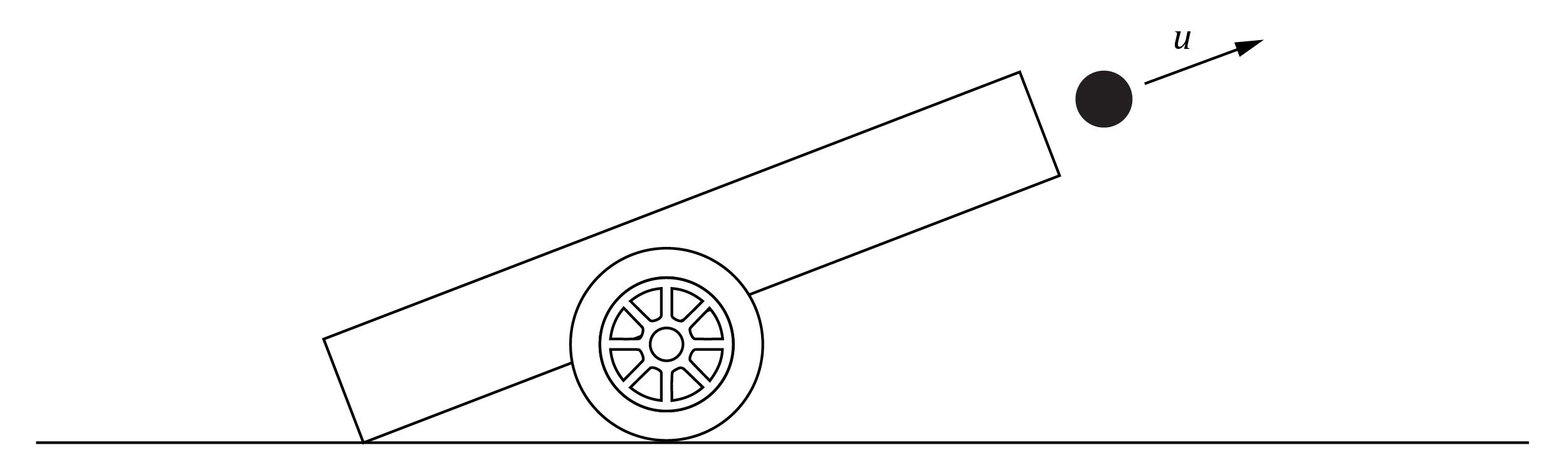
Which of the following correctly describes the kinetic energy of the ball at its maximum height?
(A) The kinetic energy is zero at its maximum height.
(B) The kinetic energy is minimum at its maximum height.
(C) The kinetic energy is maximum at its maximum height.
(D) The kinetic energy at the maximum height is greater than the kinetic energy immediately after launch.
Question 3
A racing car is travelling at a constant speed on a banked track as shown.
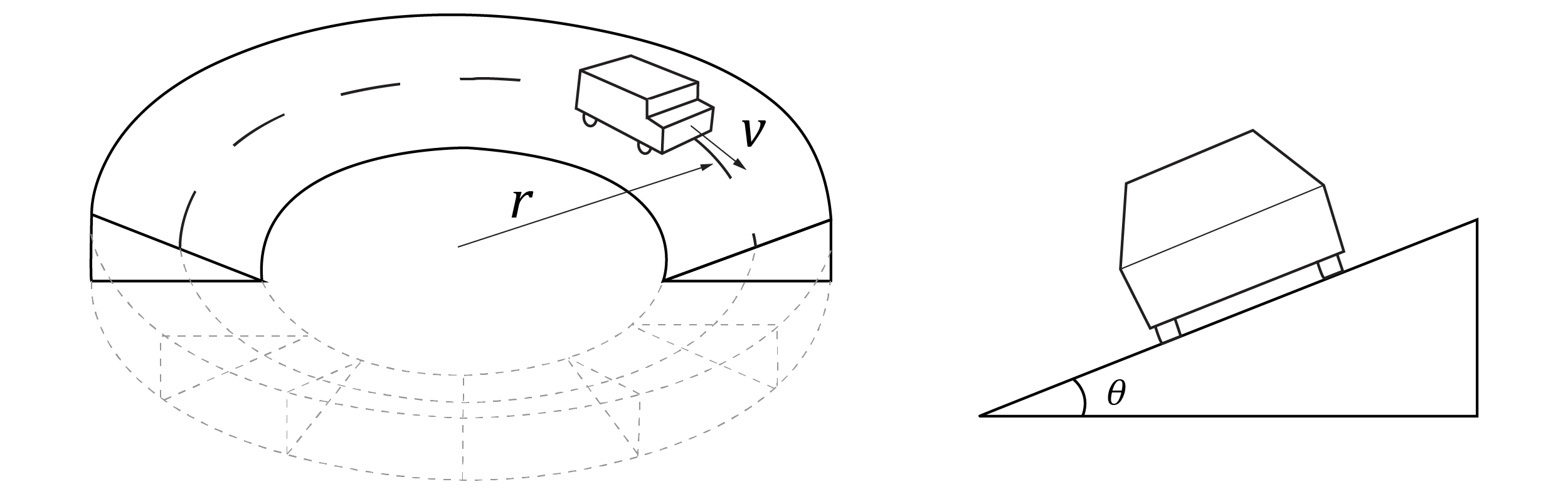
Which of the following represents the acceleration and velocity of the car?
(A) a = gtan \theta and v = rgtan \theta
(B) a = Nsin \theta and v = rgtan \theta
(C) a = gtan \theta and v = \sqrt{rgtan \theta}
(D) a = Nsin \theta and v = \sqrt{rgtan \theta}
Question 4
A student carried out an experiment to investigate the relationship between the torque produced by a force and the angle at which the force is applied. A constant force F was applied to the same position on the handle of a spanner as shown.
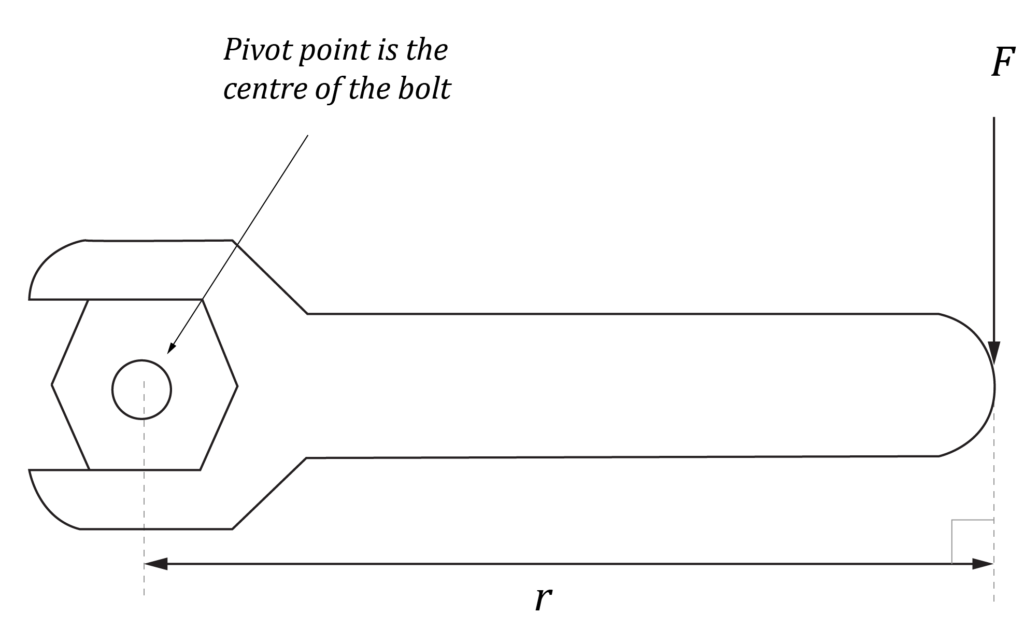
As the spanner rotated, a high-precision torque meter measured the torque experienced by the bolt.
Which of the following is correct regarding the torque acting on the bolt?
(A) The torque increases linearly as the spanner rotates.
(B) The torque decreases linearly as the spanner rotates.
(C) The torque increases sinusoidally as the spanner rotates.
(D) The torque decreases sinusoidally as the spanner rotates.
Question 5
The orbit of Halley’s Comet is shown below.
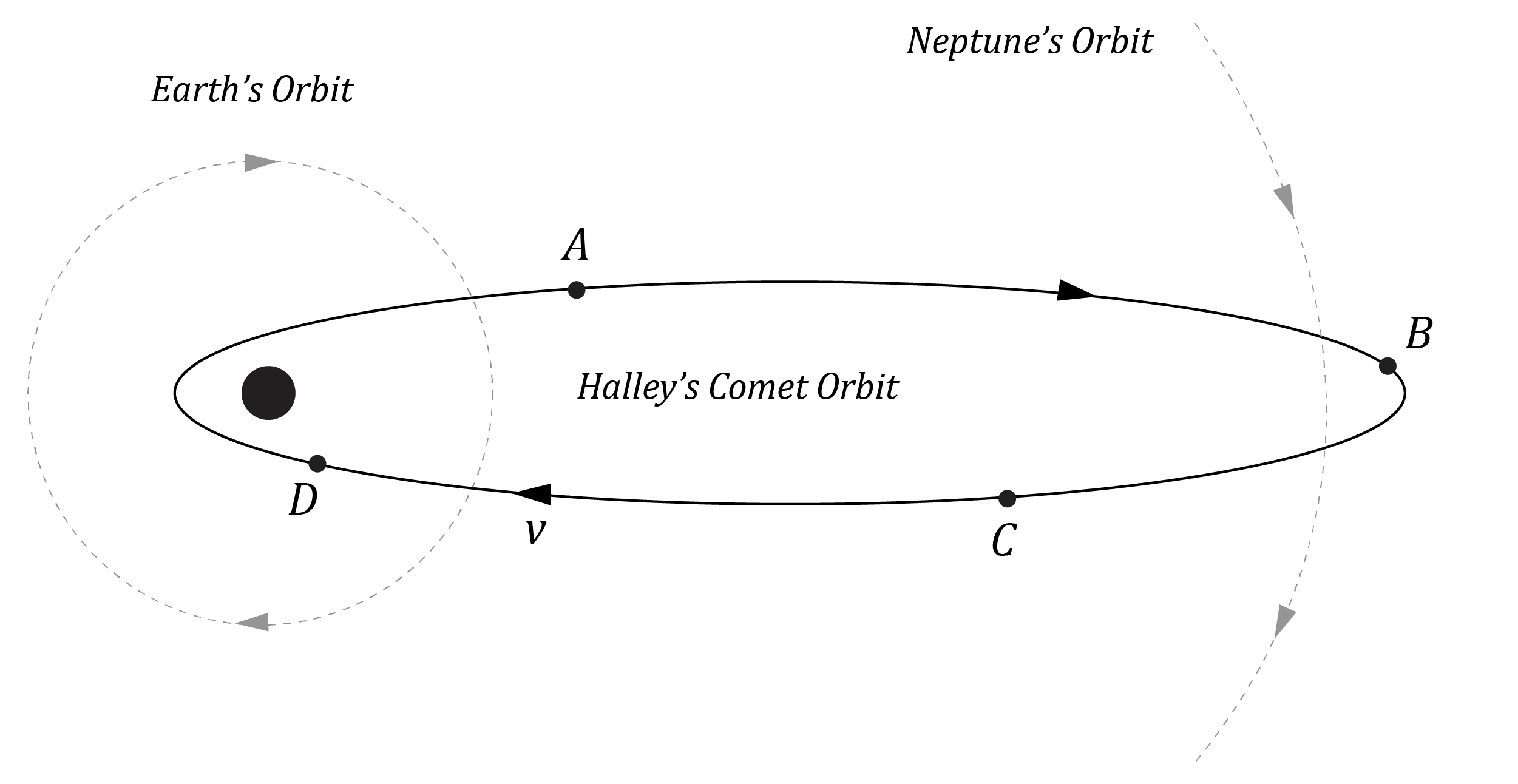
Which of the following regarding the velocity of Halley’s Comet and its total mechanical energy is correct?
| Velocity of Halley’s Comet | Total Energy E of Halley’s Comet | |
| (A) | v_B > v_C > v_A > v_D | E_A > E_B > E_C > E_D |
| (B) | v_D > v_A > v_C > v_B | E_A > E_B > E_C > E_D |
| (C) | v_B > v_C > v_A > v_D | E_A = E_B = E_C = E_D |
| (D) | v_D > v_A > v_C > v_B | E_A = E_B = E_C = E_D |
Question 6
Saturn has a mass of 5.6836 \times 10^{26} \ kg and a rotational period of 10.55 hours. What is the radius of a Saturn stationary orbit?
(A) 1.385 \times 10^{24} \ m
(B) 1.177 \times 10^{12} \ m
(C) 1.069 \times 10^{17} \ m
(D) 1.115 \times 10^8 \ m
Question 7
A charged oil drop of mass m is placed between two parallel, horizontal plates in a vertical plane as shown.
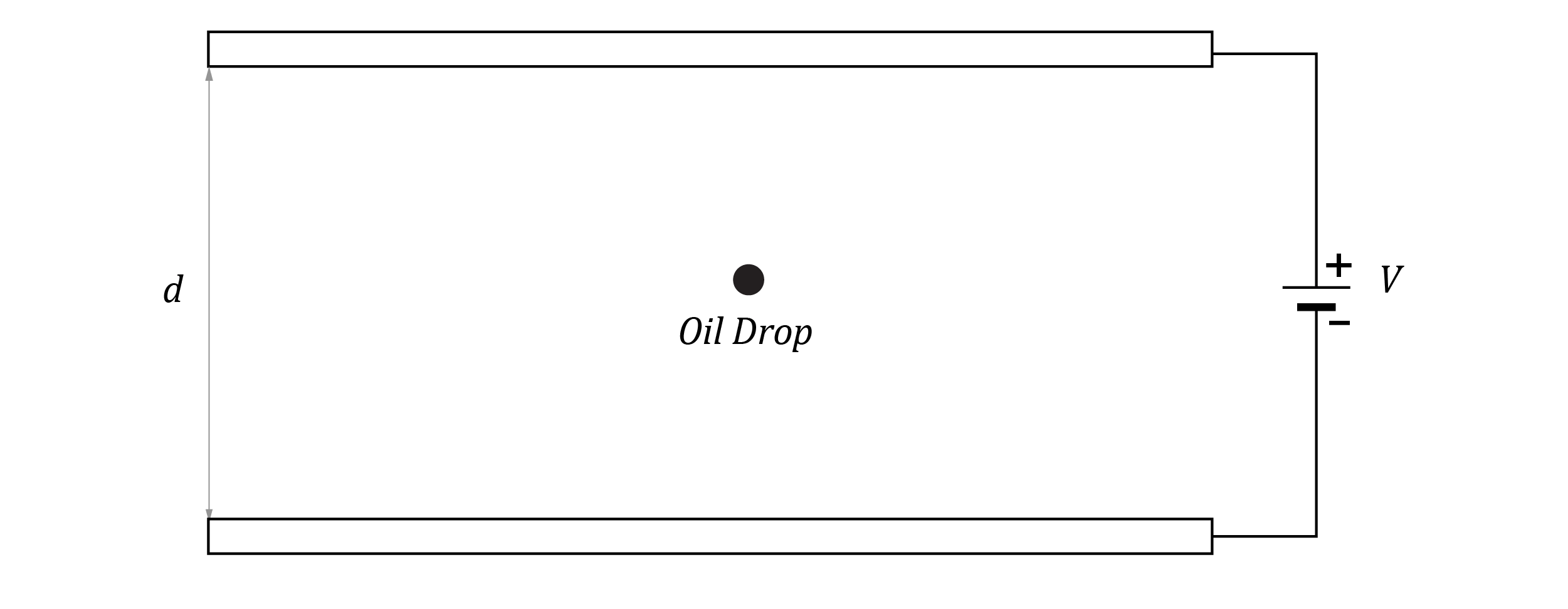
The potential difference between the plates is adjusted until the charge is stationary. What is the expression for the potential difference between the plates?
(A) V = \dfrac{mgd}{q}
(B) V = \dfrac{q}{mgd}
(C) V = \dfrac{mgq}{d}
(D) V = \dfrac{d}{mgq}
Question 8
The diagram below shows observations of the spectrum of a star.
Which of the following explains the changes in the spectrum during the period shown?
(A) The star is moving away from the Earth.
(B) The star is moving towards the Earth.
(C) The star is rotating about its axis.
(D) The star is both moving away from the Earth and moving toward the Earth.
Question 9
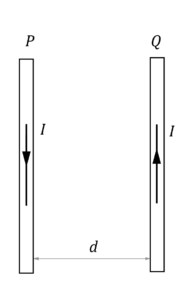
Current flows in two wires P and Q as shown in the diagram.
Which of the following correctly predicts the magnetic field direction and force direction at P due to the current in Q?
| Field direction at P due to current in Q | Force direction on P due to current in Q | |
| (A) | Into the page | Right and towards Q |
| (B) | Out of the page | Right and towards Q |
| (C) | Into the page | Left and away from Q |
| (D) | Out of the page | Left and away from Q |
Question 10
A straight wire and circular loop of wire are placed next to each other as shown.
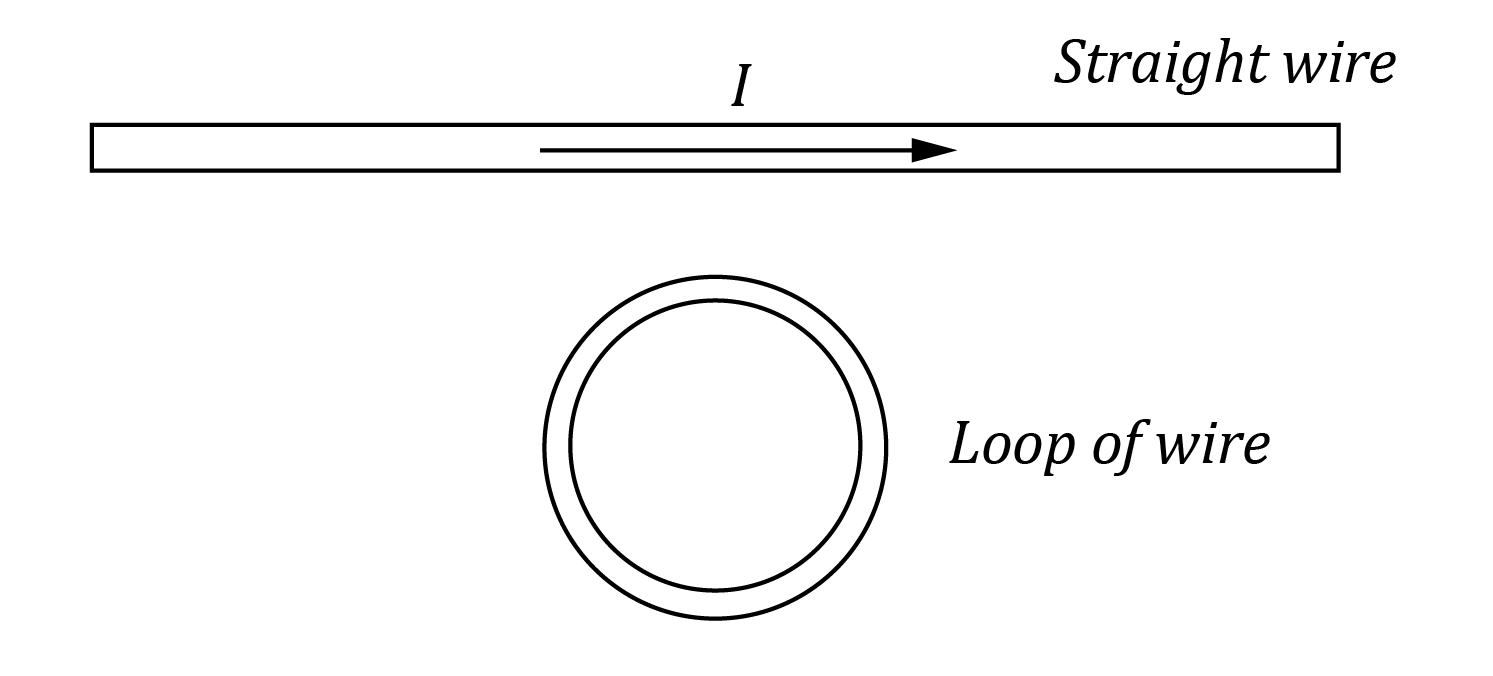
The current in the straight wire flows to the right.
What is the direction of the induced current in the circular loop of wire if the current in the straight wire decreases with time?
(A) Zero
(B) Clockwise
(C) Anti-clockwise
(D) Alternating
Question 11
A beam of unpolarised light is incident on two parallel polarisers as shown.
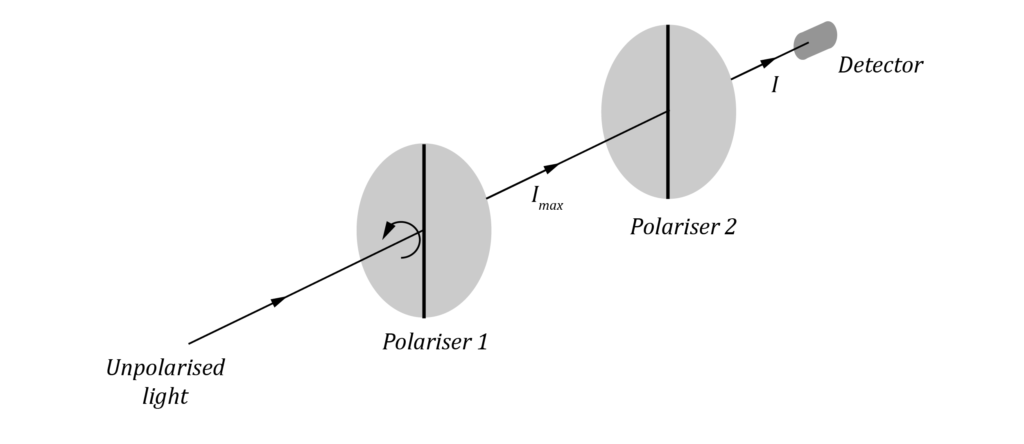
Initially, the transmission axes of the polarisers are parallel.
The first polariser is now rotated anticlockwise by 45 degrees. What is the result of this rotation on the intensity and the polarisation axis of the transmitted light I compared to I_{max} ?
| Intensity of transmitted light | The axis of polarisation of the transmitted light | |
| (A) | 0.5 \ I_{max} | 45 \degree clockwise |
| (B) | 0.5 \ I_{max} | 45 \degree anticlockwise |
| (C) | 0.7 \ I_{max} | 45 \degree clockwise |
| (D) | 0.7 \ I_{max} | 45 \degree anticlockwise |
Question 12
Proxima Centauri is a red-dwarf star in the Alpha Centauri system. It emits electromagnetic radiation with a peak wavelength of 953 \ nm .
A student makes the following predictions about Proxima Centauri.
(1) It has a surface temperature of 3040 K.
(2) The star is a perfect emitter of electromagnetic radiation.
(3) The star is a perfect absorber of electromagnetic radiation.
Which of the following predictions about Proxima Centauri are correct?
(A) (1) and (2) only
(B) (1) and (3) only
(C) (2) and (3) only
(D) (1), (2), (3)
Question 13
A schematic diagram of a photoelectric effect experiment is shown below. When UV light illuminates a metal surface, photoelectrons are emitted.
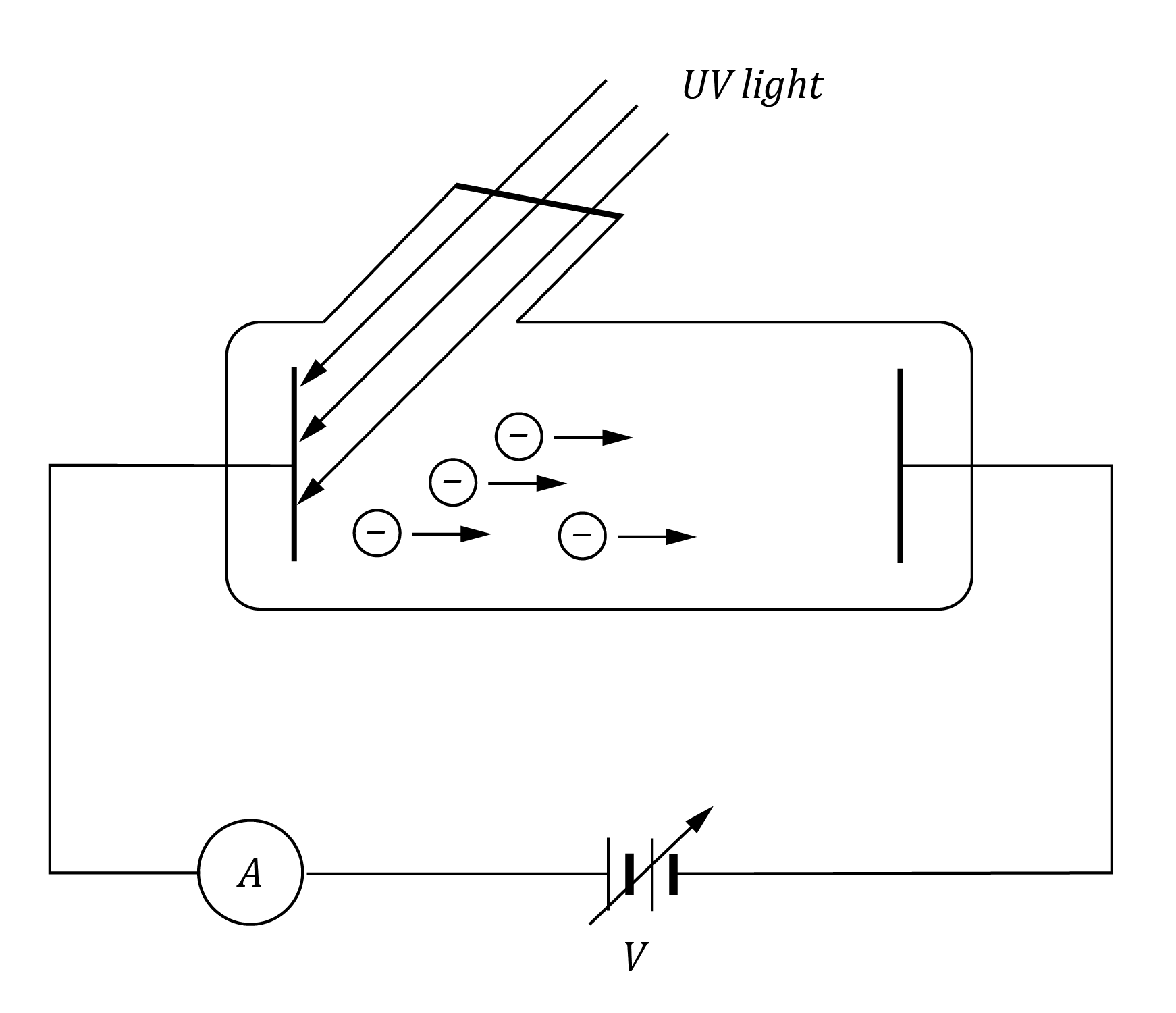
Which of the following changes could cause the photocurrent to stop?
(A) Increasing the potential difference of the power supply.
(B) Increasing the frequency of the UV light.
(C) Increasing the intensity of the UV light.
(D) Changing the metal surface to one with a smaller work function.
Question 14
Which of the following best describes the method Hertz used to prove that radio waves travel at the speed of light as theorised by Maxwell?
(A) By reflecting the radio waves and measuring the wavelength setup by diffraction.
(B) By reflecting the radio waves and measuring the wavelength setup by interference.
(C) By reflecting the radio waves and measuring the distance between the antinode of standing waves setup by diffraction.
(D) By reflecting the radio waves and measuring the distance between the antinodes of standing waves setup by interference.
Question 15
The diagram shows a DC motor with curved magnets and a constant current flowing to the rotor.
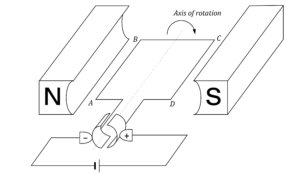
Which pair of graphs best describes the behaviour of the force F on wire AB, and the torque \tau on the rotor as functions of time t?
| Force vs Time | Torque vs Time | |
| (A) | 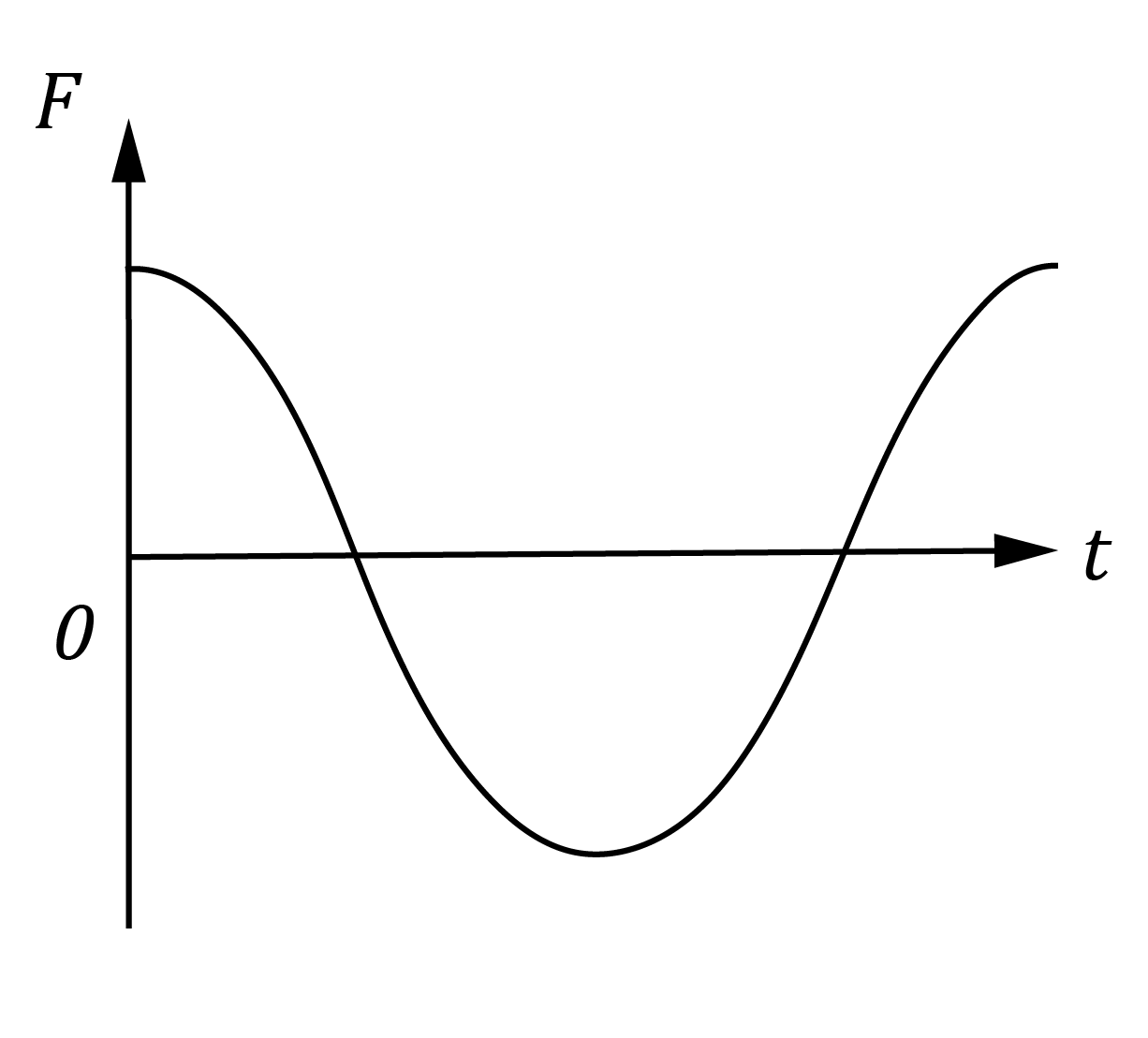 | 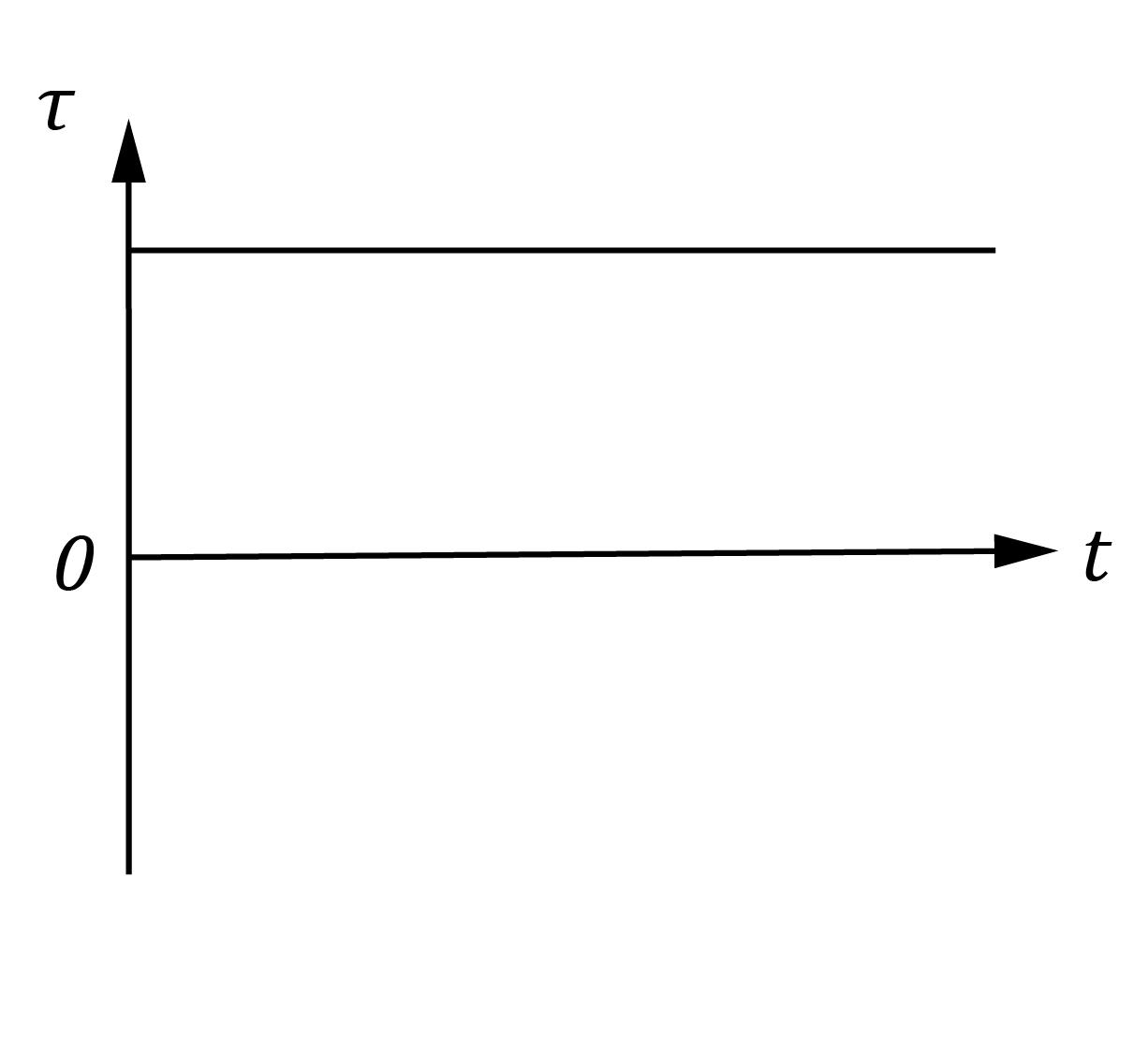 |
| (B) | 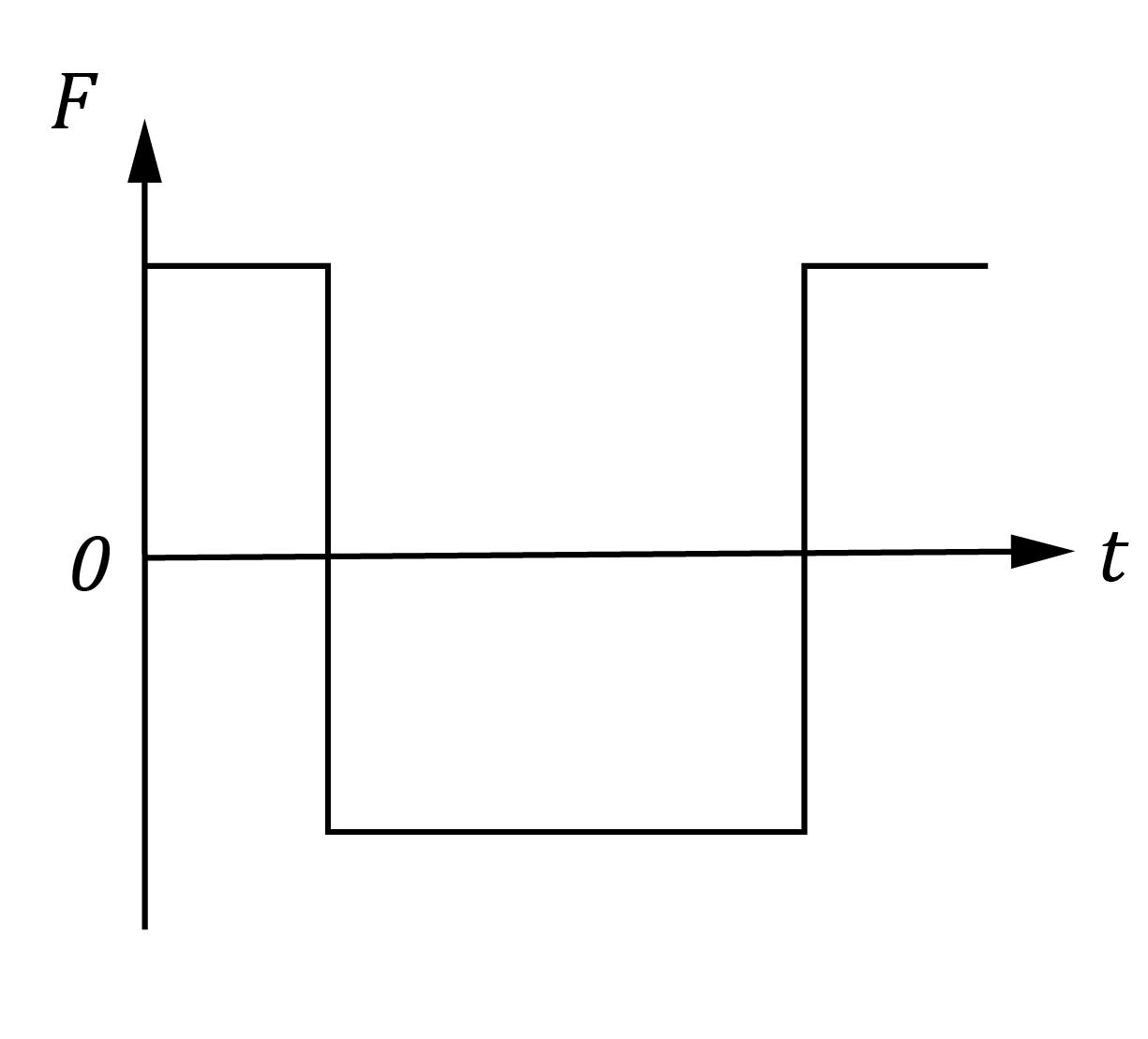 | 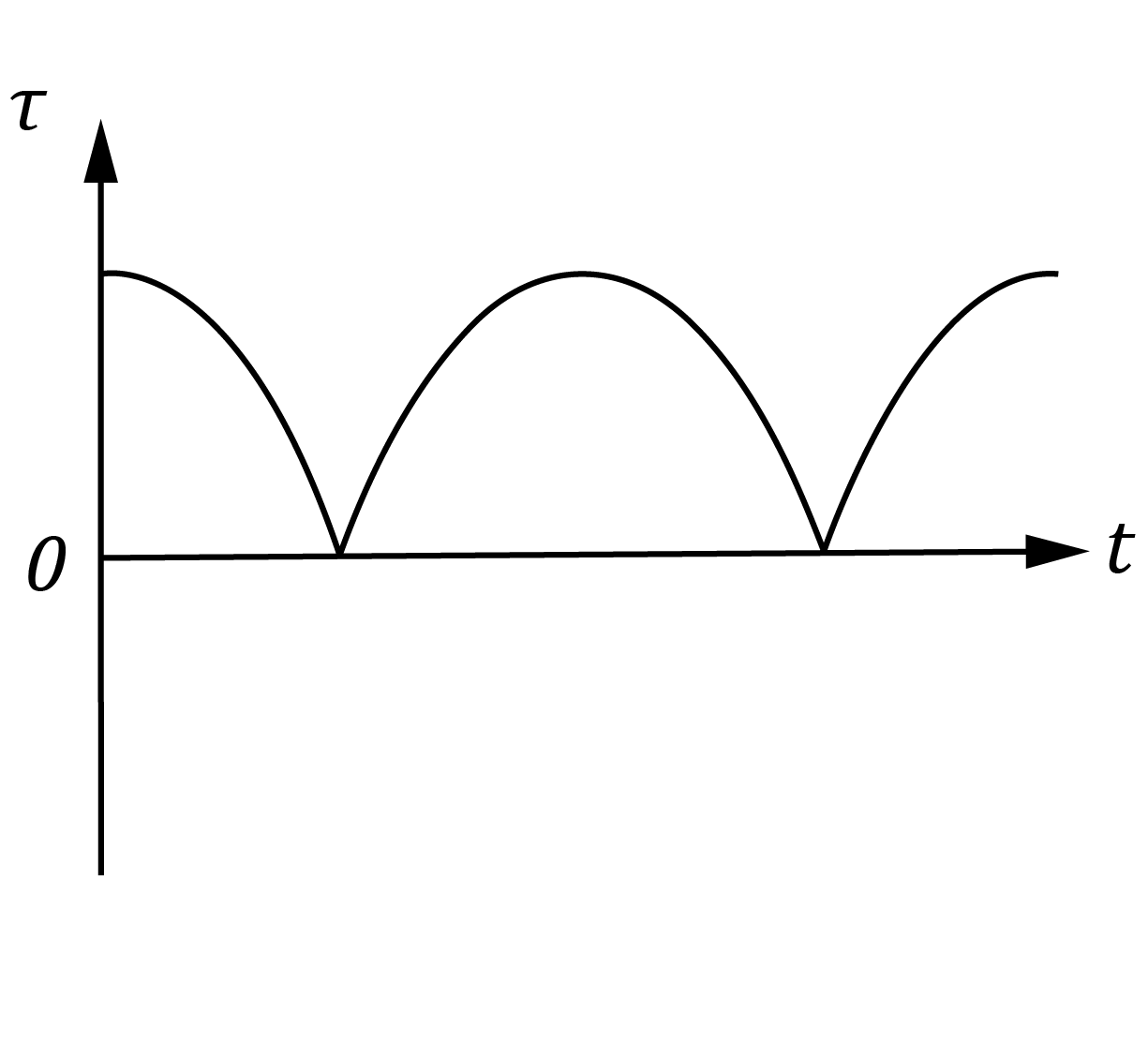 |
| (C) | 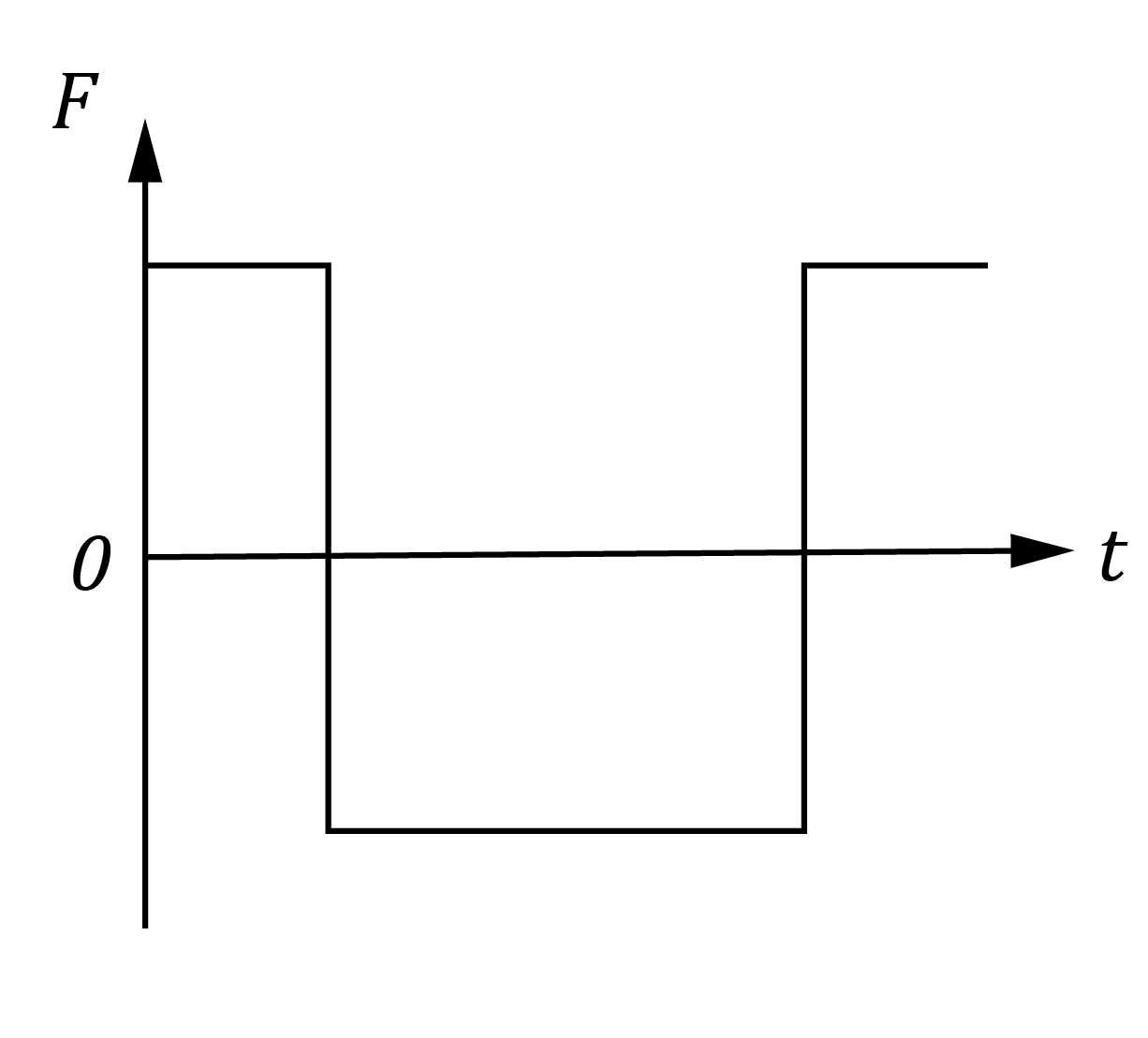 | 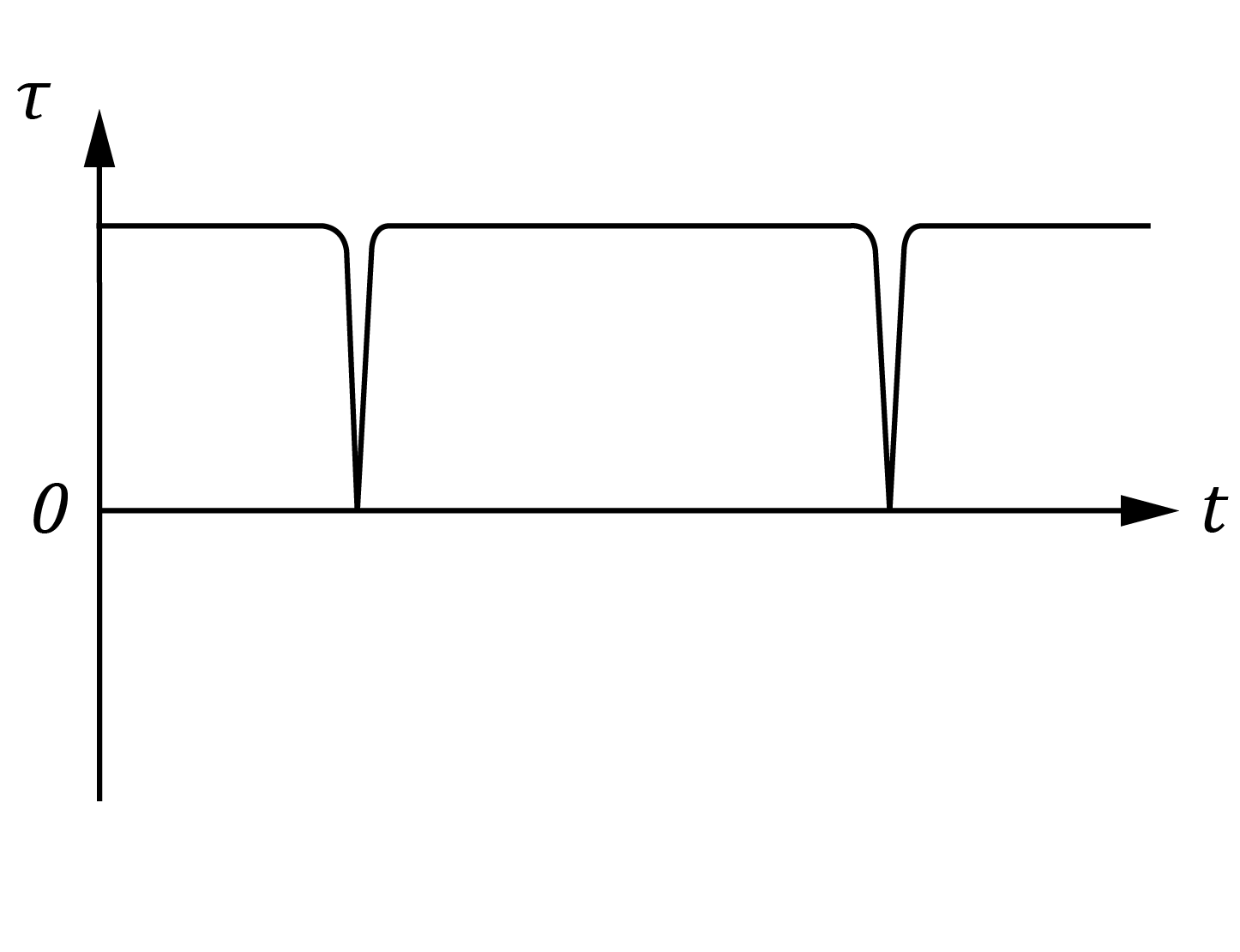 |
| (D) | 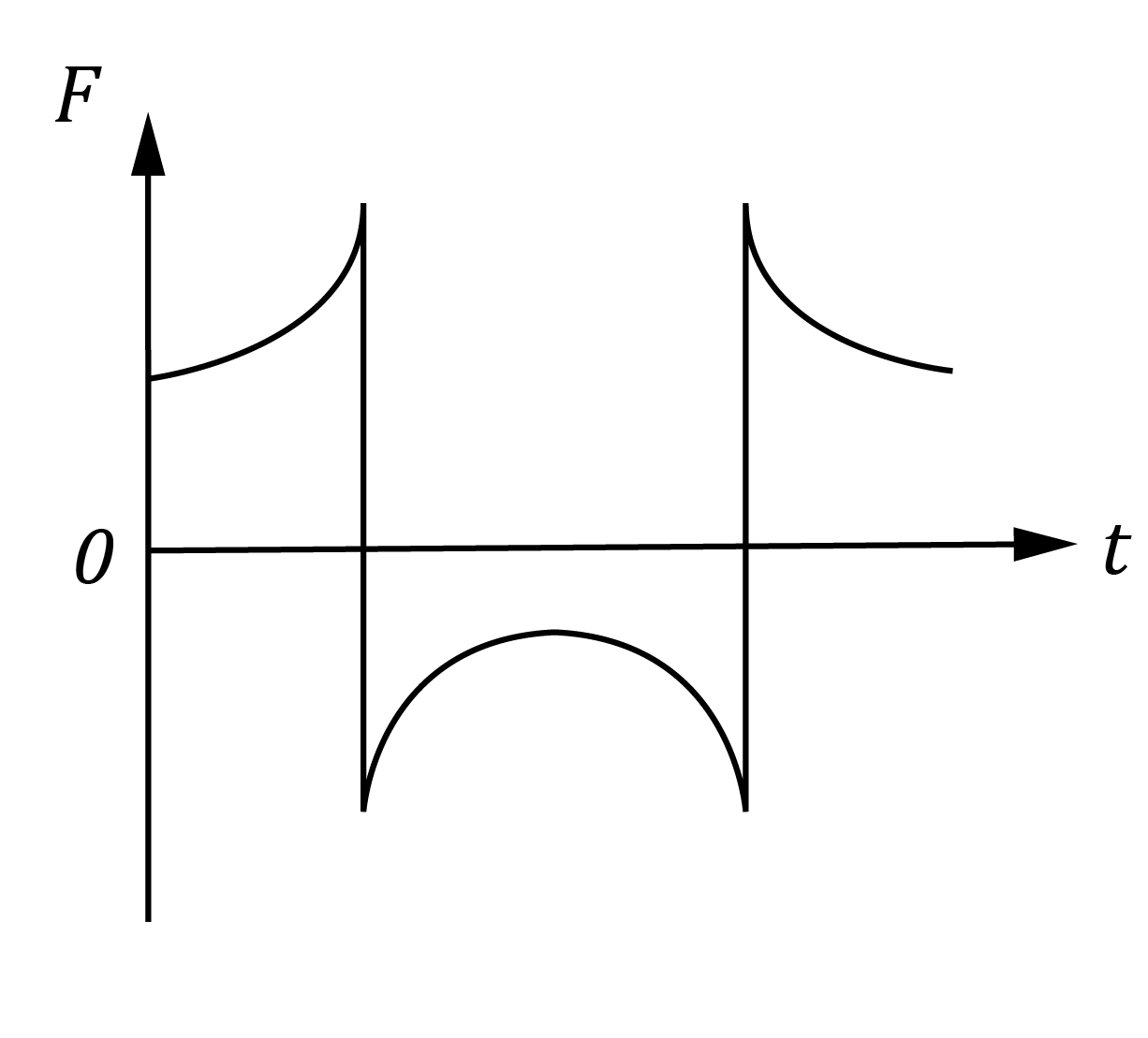 |  |
Question 16
A student aims to determine the acceleration of a non-inertial frame of reference using a mass suspended from the ceiling of a model train carriage. When the train is accelerating along a straight horizontal surface, the string makes an angle with the vertical as shown.
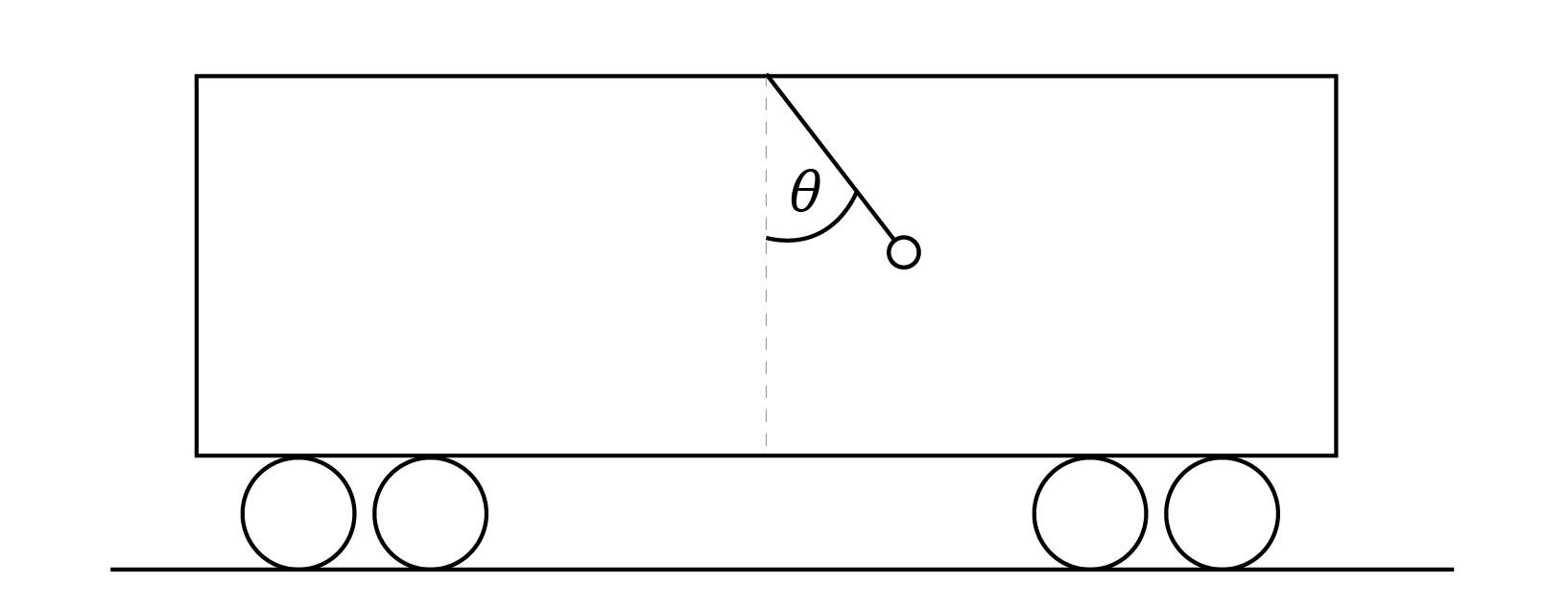
Which of the following represents the magnitude of the acceleration of the train?
(A) a = gsin \theta
(B) a = \dfrac{g}{sin \theta}
(C) a = gtan \theta
(D) a = \dfrac{g}{tan \theta}
Question 17
The graph below shows the change in magnetic flux through a coil of wire against time.
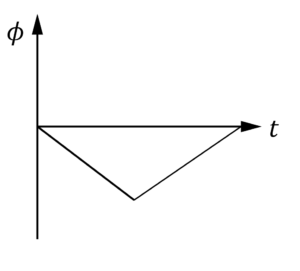
Which one of the of the following graphs best represent how the induced EMF across the coil of wire varies with time?
| (A) | 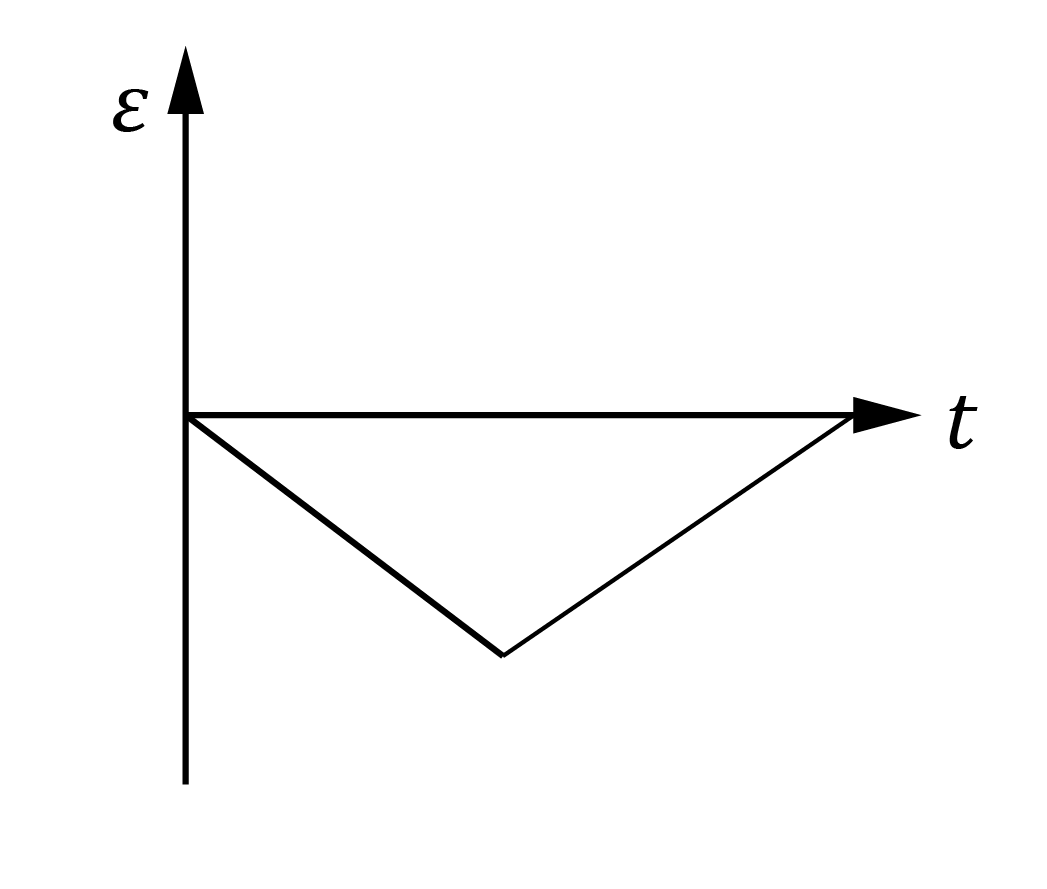 | (B) | 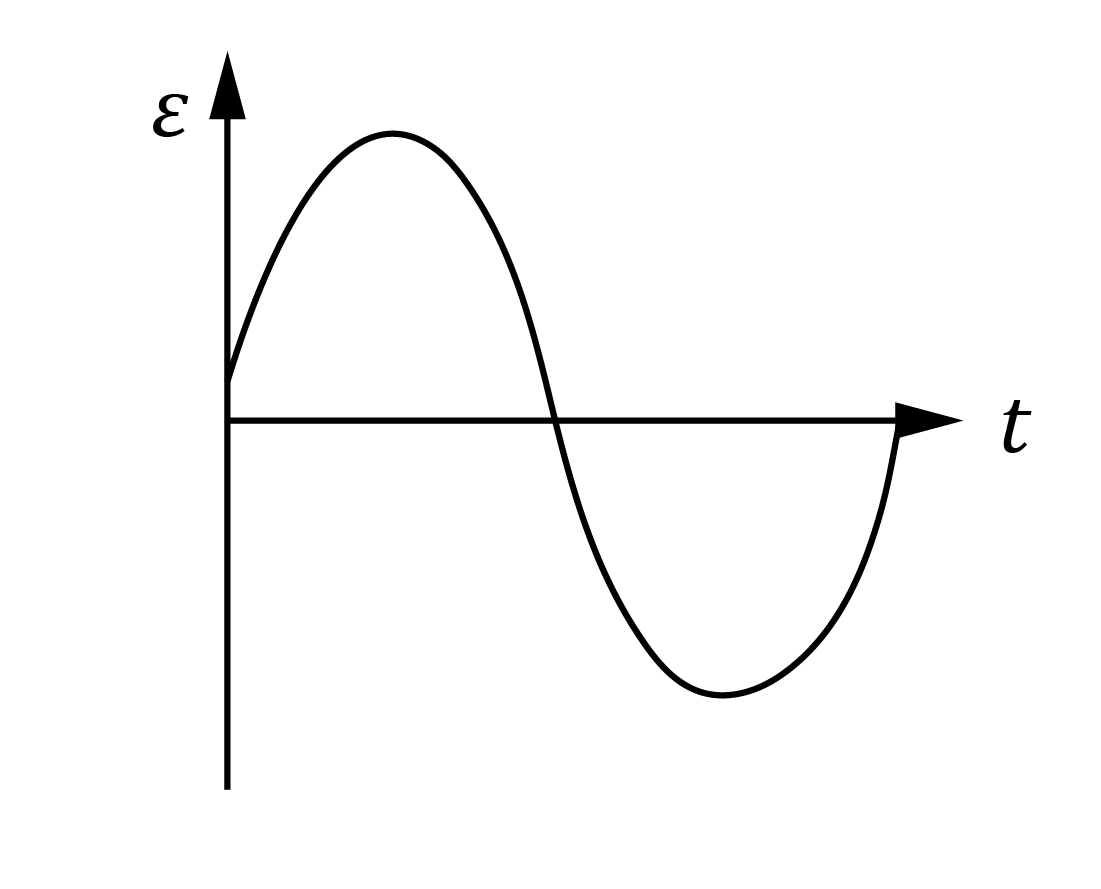 |
| (C) | 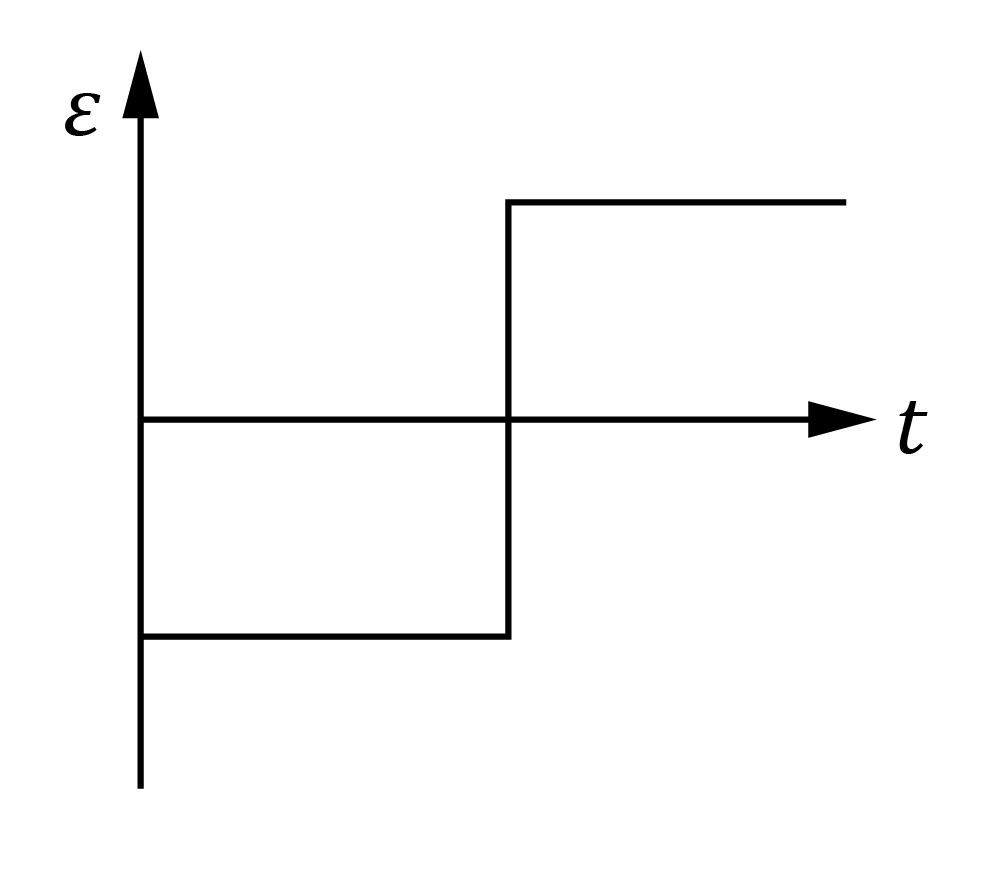 | (D) | 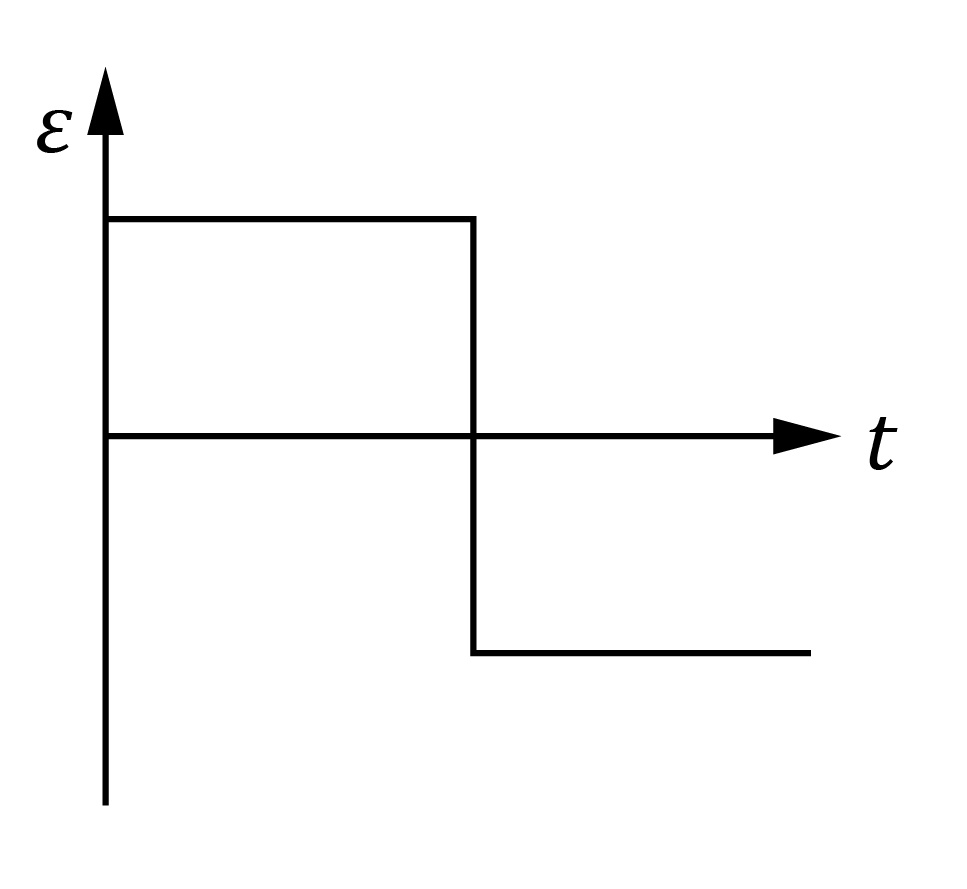 |
Question 18
An electric field accelerates a proton from rest between two parallel plates inside a discharge tube. The proton exits into a region of uniform magnetic field strength of \vec{B} = 0.10 \ T perpendicular to its path, as shown in the diagram below.
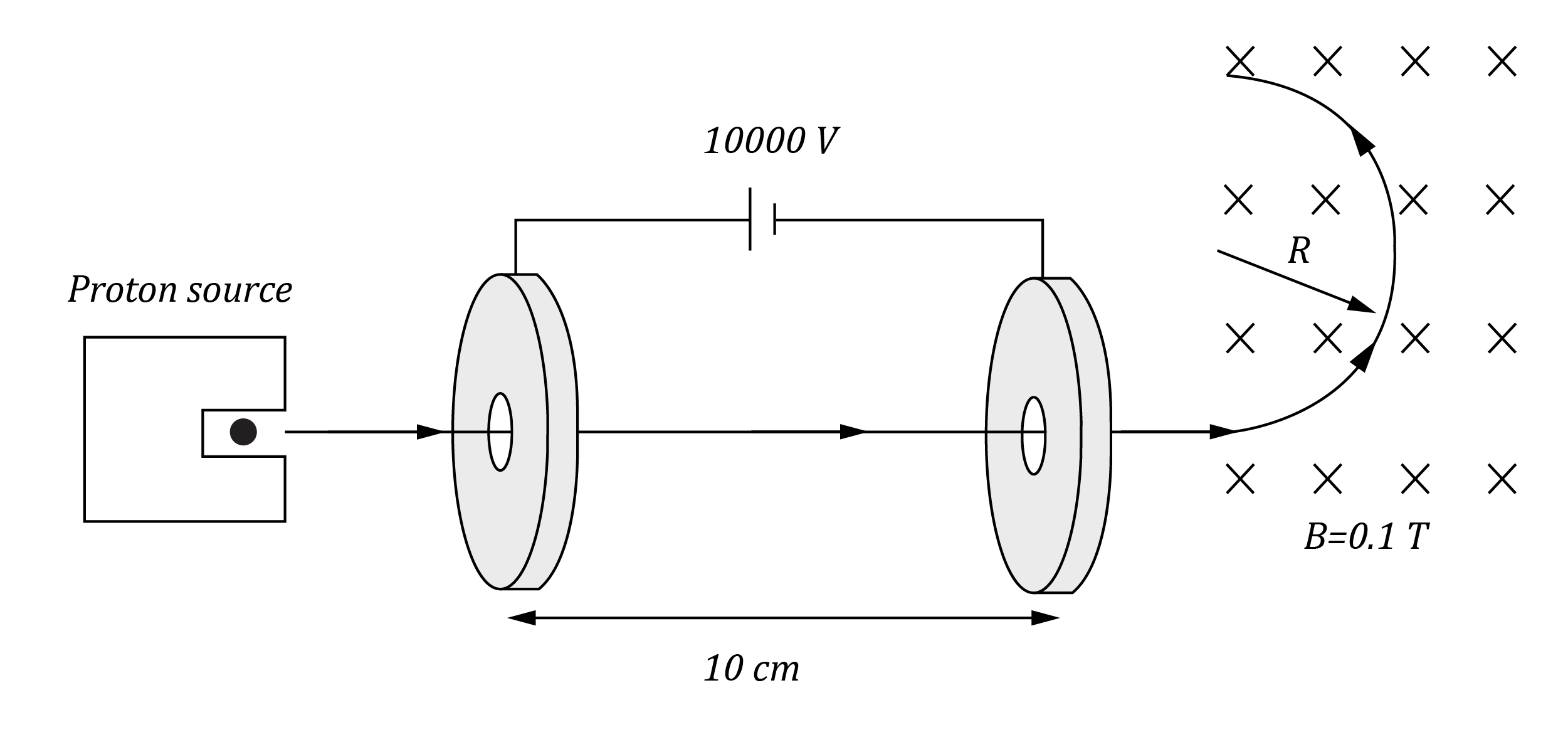
Calculate the radius R of the deflection of the proton’s path in the magnetic field.
(A) 3.4 x 10-3 m
(B) 0.14 m
(C) 0.15 m
(D) 6.9 m
Question 19
A UV Lamp emits a wavelength of 400 \ nm . Calculate the minimum number of photons required to transfer at least 31 \ eV of energy.
(A) 1
(B) 10
(C) 6.238 \times 10^{19}
(D) 6.238 \times 10^{28}
Question 20
An ideal transformer has 100 primary turns of winding and 10 turns of secondary winding. The current in the primary is 2 A and the input power to the primary is 10 W.
Which one of the following statements regarding the secondary current and the secondary power output is true?
(A) I_s = 20 \ A and P_s = 1.0 \ W
(B) I_s = 0.2 \ A and P_s = 10 \ W
(C) I_s = 0.2 \ A and P_s = 100 \ W
(D) I_s = 20 \ A and P_s = 10 \ W
End of Section I
Section II: Extended Response Questions
In Section II of Mock Physics Trial Paper:
- There are 15 Extended Response Questions.
- Allow 2 hours 25 minutes for this section.
Question 21 (3 marks)
A ball is released from rest and rolls down a frictionless smooth curved ramp from point P as shown.
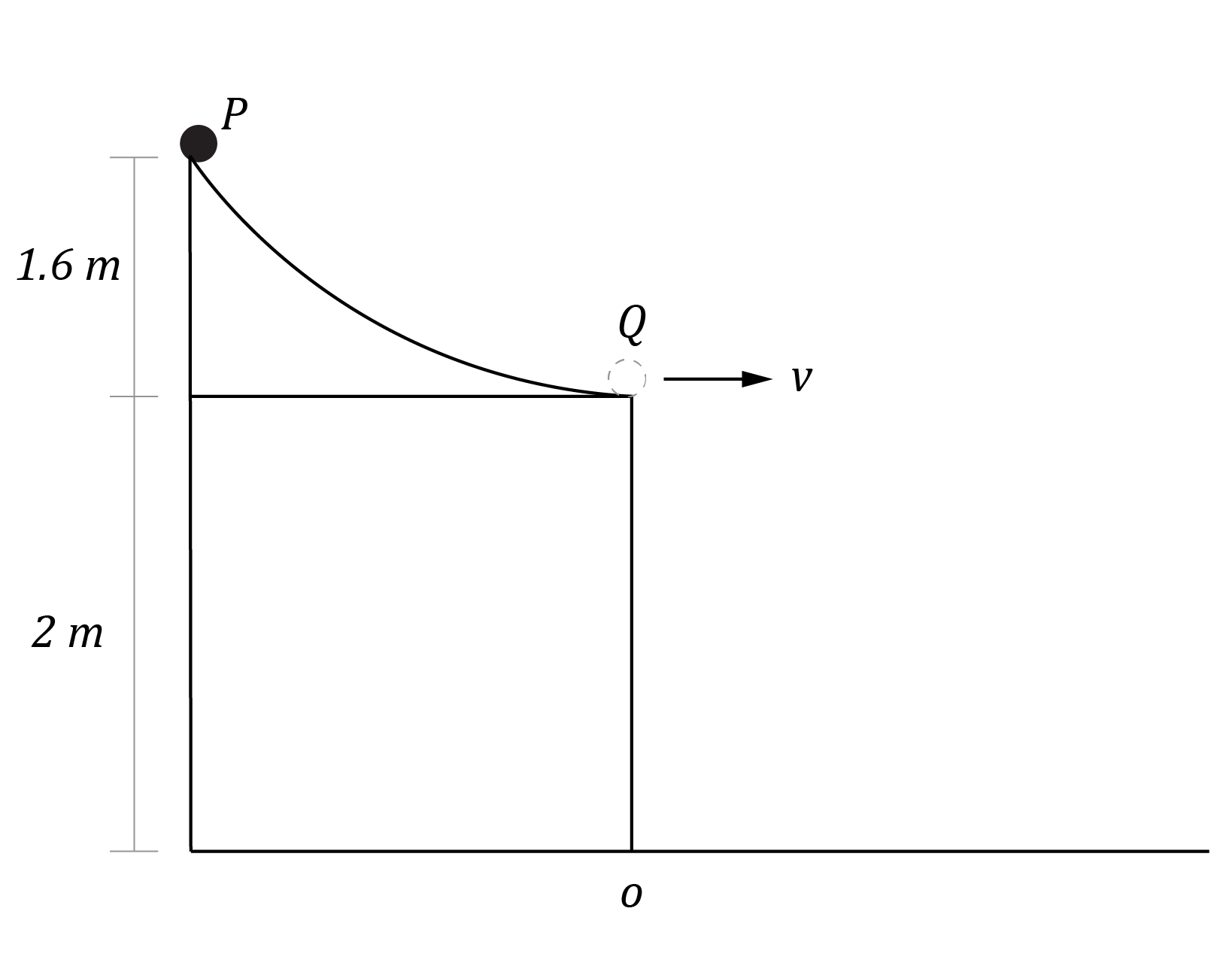
When the ball reaches the bottom of the ramp, it travels horizontally.
| (a) | Calculate the velocity of the ball at the bottom of the ramp. | 1 |
| (b) | Calculate the horizontal distance from point O at which the ball will hit the floor. | 2 |
Question 22 (6 marks)
The diagram shows a conical pendulum consisting of a ball of mass 100 g on the end of a string of length 0.5 m.
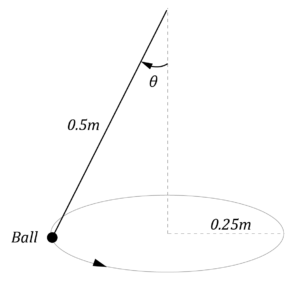
It traces out a circular path of radius 0.25 m.
| (a) | Calculate the angular speed of the ball. | 3 |
| (b) | Calculate the period of the conical pendulum. | 1 |
| (c) | Explain the effect of increasing the radius on the period of the conical pendulum. | 2 |
Question 23 (7 marks)
A loop-de-loop track is shown below. The loop in the track has a radius of 39.2 m.
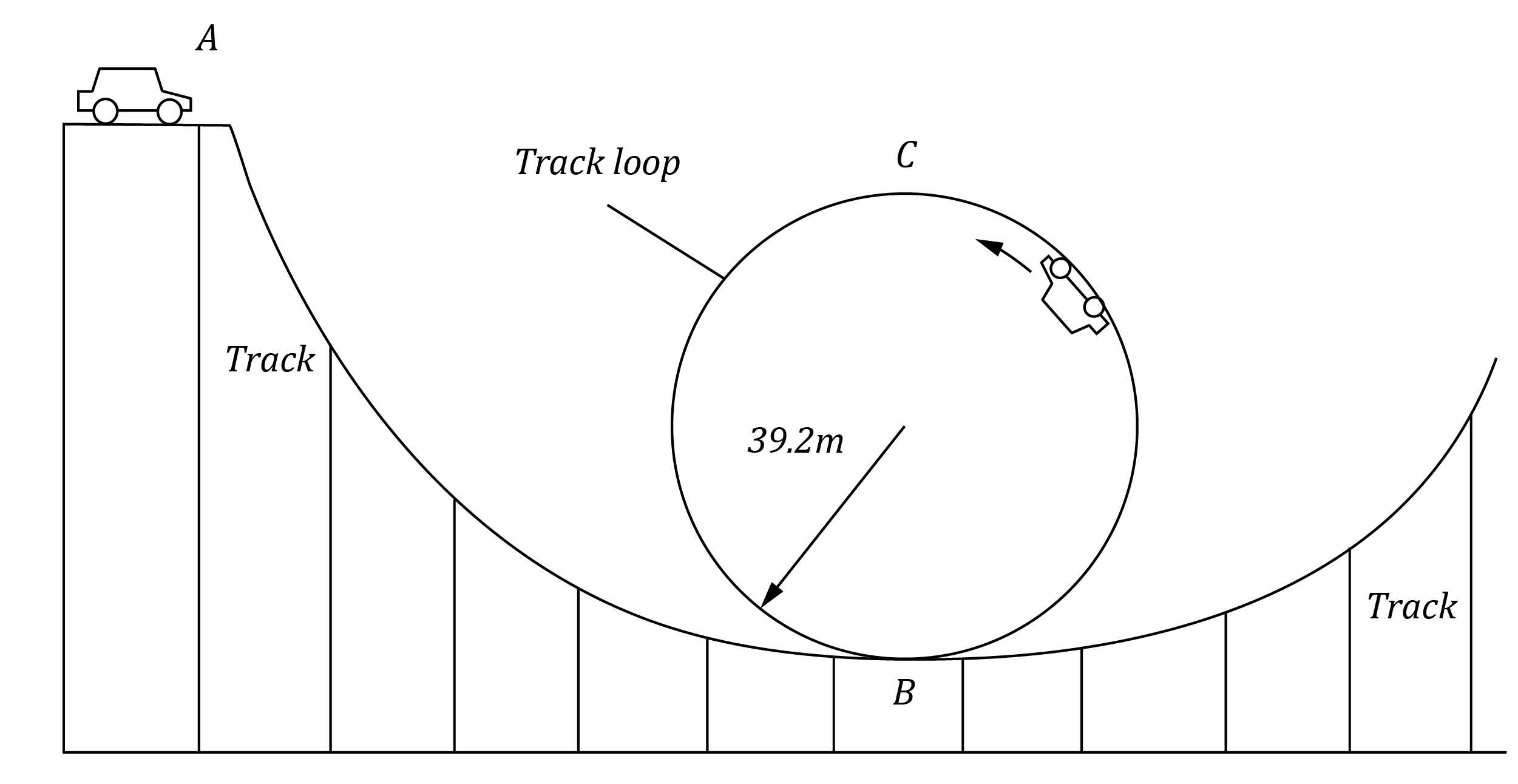
In order to complete the loop-de-loop safely, the car must not lose contact with the track when travelling over the top of the loop, point C. Ignore the effects of air resistance and friction.
| (a) | Calculate the minimum speed that the car and the rider must have at point C so that it does not leave the track. | 3 |
| (b) | Hence or otherwise, calculate the speed the car needs when entering the bottom of the loop, point B. | 2 |
| (c) | Hence or otherwise, calculate the minimum height h of the rollercoaster track at point A above point B to ensure the car and the rider completes the loop-de-loop. | 2 |
Question 24 (8 marks)
A spaceship of mass m is moving at speed v in a circular orbit of radius r around a planet of mass M .
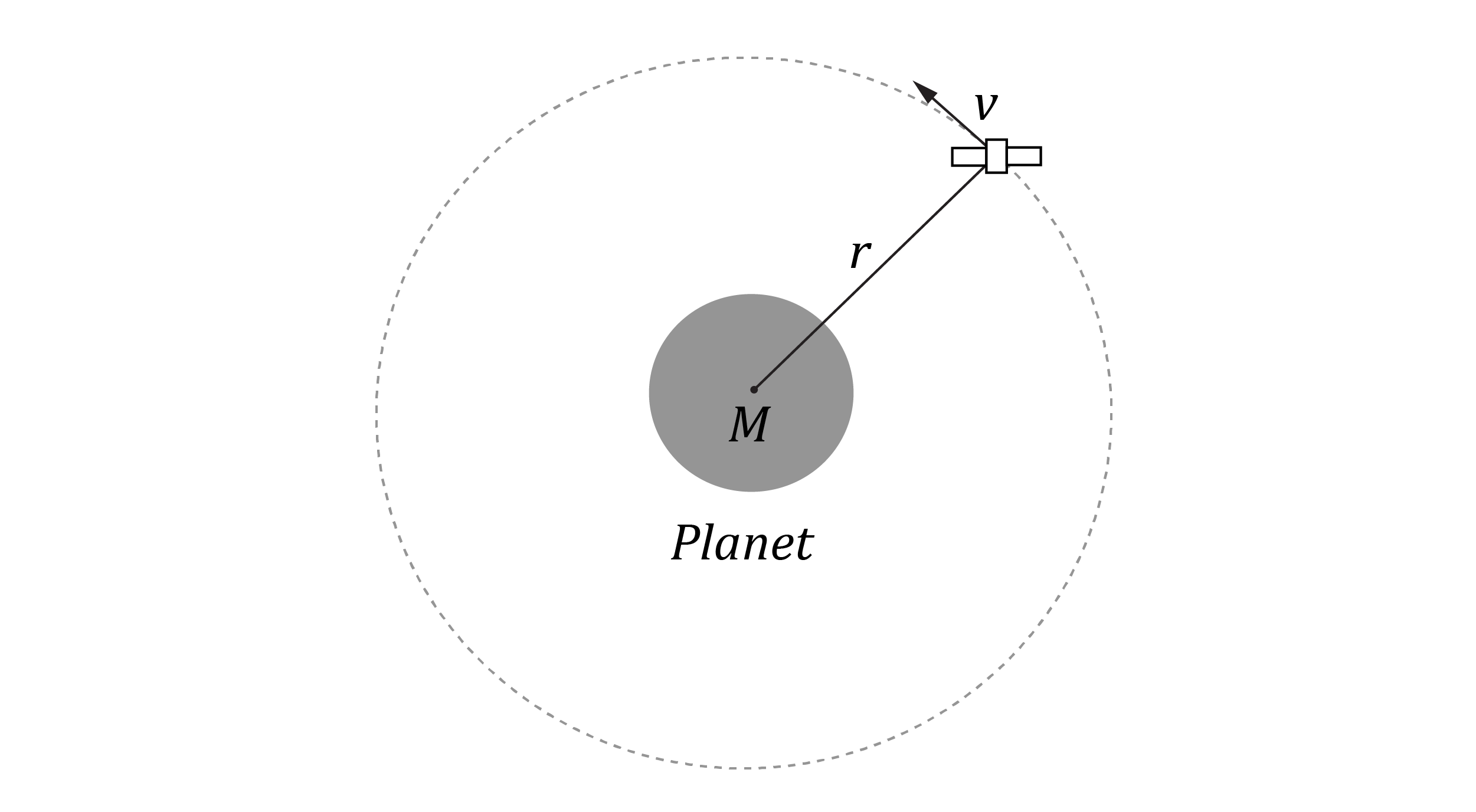
| (a) | Identify the force that allows the spaceship to accelerate around the planet. | 1 |
| (b) | Astronauts inside the spaceship experience apparent weightlessness, even though there is a force acting on them. Explain. | 2 |
| (c) | Show that the spaceship’s total energy in an orbit is given by E = -\dfrac{GMm}{2r} . Comment on the negative sign on the total energy of the spaceship. | 3 |
| (d) | The spaceship encounters friction. Explain the effect the frictional force has on the total energy of the spaceship | 2 |
Question 25 (4 marks)
An electron moving with speed v enters a uniform electric field of strength E and a uniform magnetic field of strength B as shown.
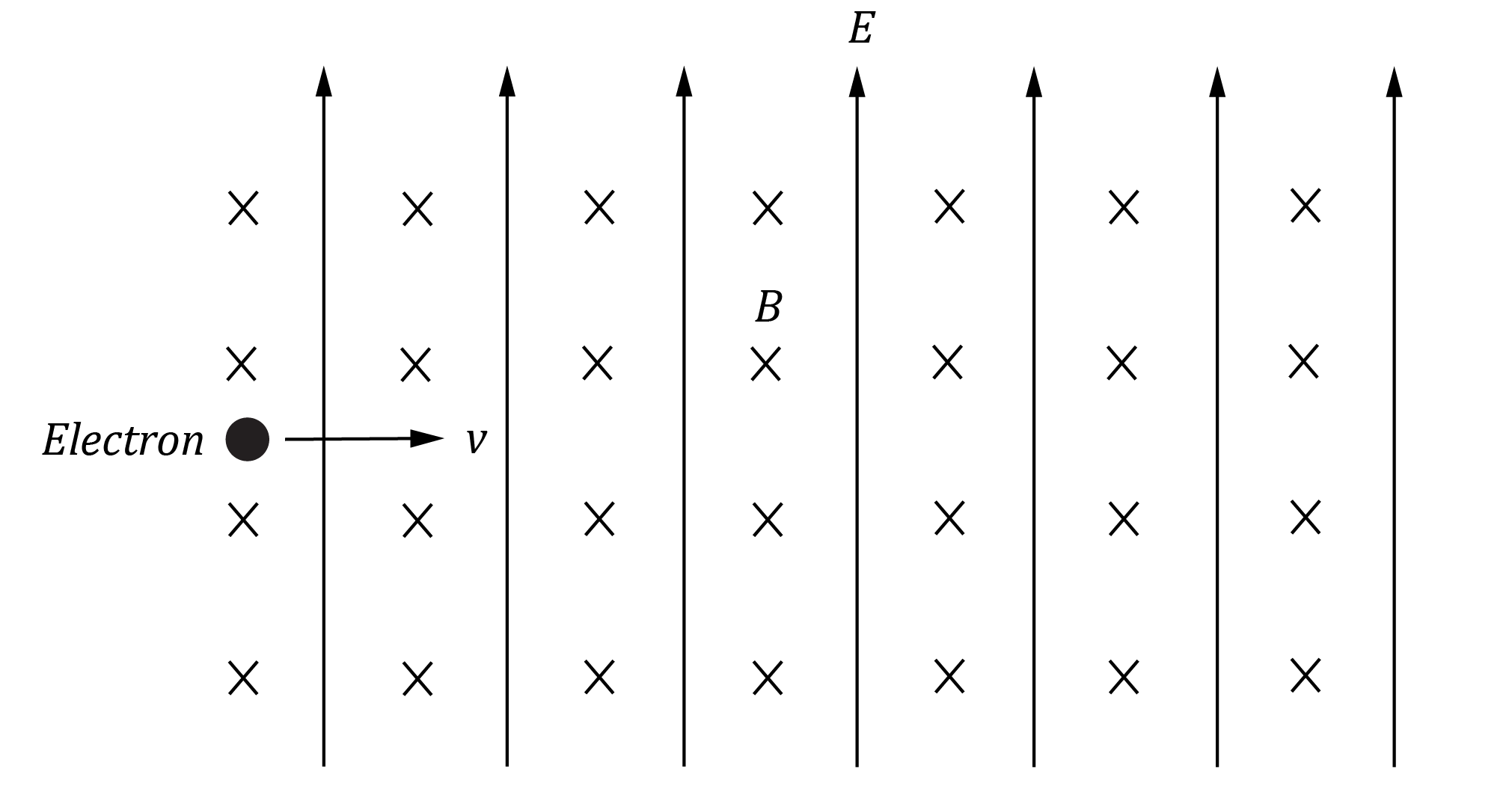
The magnetic field is directed into the page and the electric field is vertically up the page.
| (a) | State the directions of the electric force and magnetic force acting on the electron. | 1 |
| (b) | Explain how the velocity of the electron entering the fields could be determined. Provide any relevant formulas. | 3 |
Question 26 (7 marks)
A magnet is suspended above a solenoid by a spring as shown.
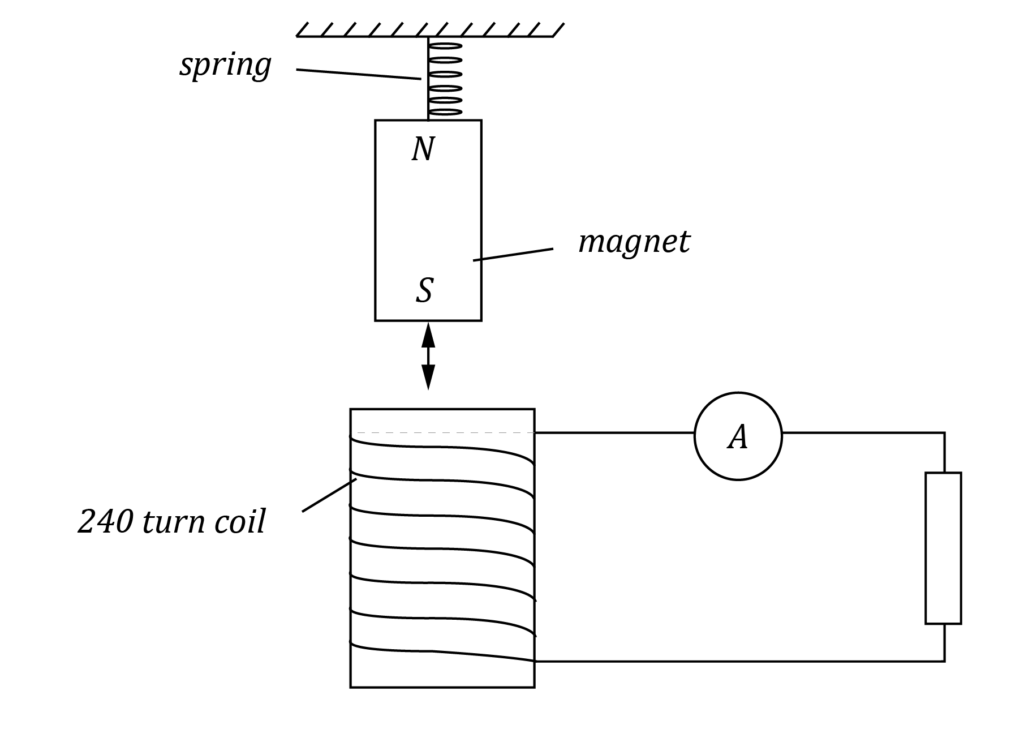
The magnet is displaced vertically down and released. The magnet takes 0.5 \ s to move between tis lowest and highest positions. Ignore any effects of air resistance and friction.
| (a) | Explain why there is an induced current in the solenoid after the magnet has been released. | 2 |
| (b) | State the direction of the induced current passing through the resistor immediately after the magnet is released. | 1 |
| (c) | The magnet comes to a stop after 4 seconds. Explain. | 2 |
| (d) | Sketch a graph to show how the induced current varies with time for the first 2 seconds. | 2 |
Question 27 (4 marks)
Many electric vehicles such as the Tesla Model 3 use regenerative braking to improve their energy efficiency.

| (a) | Explain how regenerative braking works. | 3 |
| (b) | Outline one major difference between regenerative braking and electromagnetic braking. | 1 |
Question 28 (4 marks)
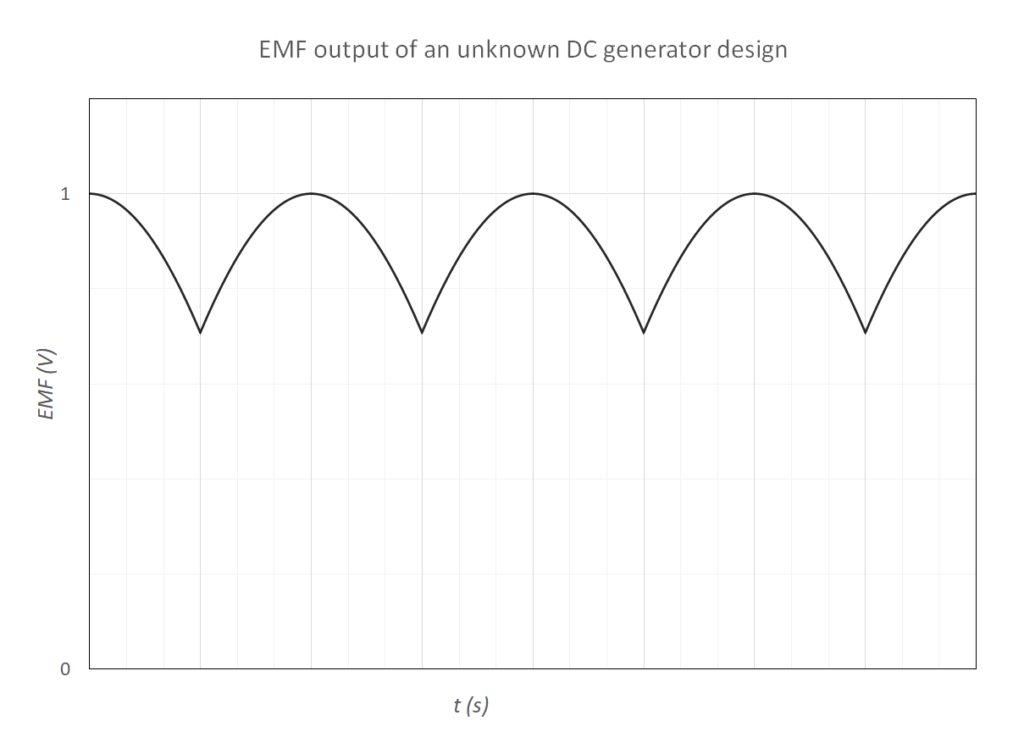
A model of a simple DC generator is shown below,
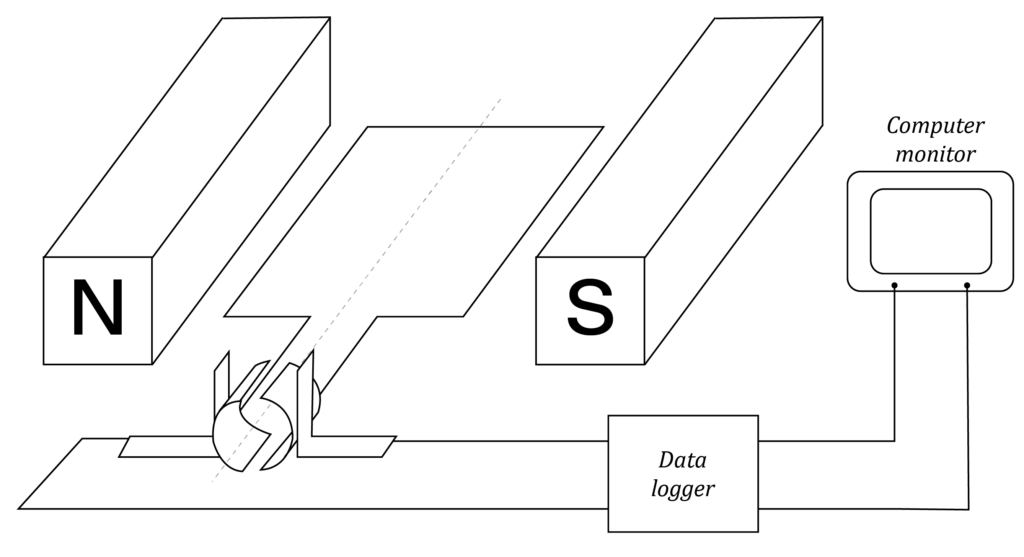
| (a) | Explain why the model shown above depicts a DC generator. | 2 |
| (b) | A graph of EMF output from an unknown DC generator design is shown below.
Explain what modification(s) can be made to the simple DC generator above in order to produce this EMF output. | 2 |
Question 29 (4 marks)
A read laser beam is shone onto two narrow slits S_1 and S_2 in a dark room, and an interference pattern of bright red and dark liens (fringes) appears on a screen, as shown below.
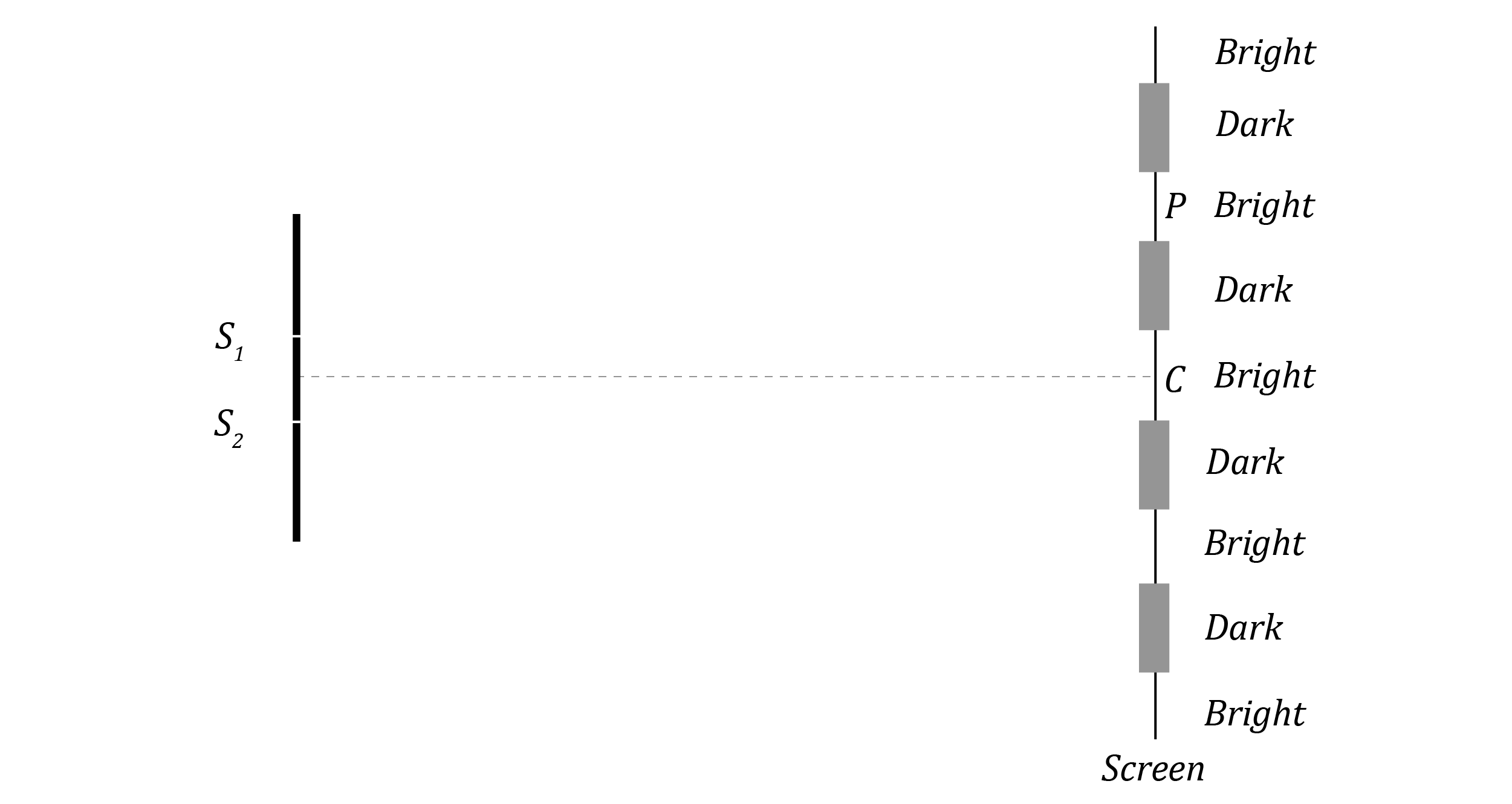
The screen is at a large distance L from the slits. C is the central bright maximum. The distance on the screen between C and P represents a distance h .
| (a) | Account for the interference pattern on the screen. | 2 |
| (b) | Describe the effect of increasing the distance between the slits S_1 and S_2 on the interference pattern. | 2 |
Question 30 (6 marks)
A plot of several experimentally measured black body radiation spectra is shown in the diagram below, together with the spectrum predicted by classical theory.
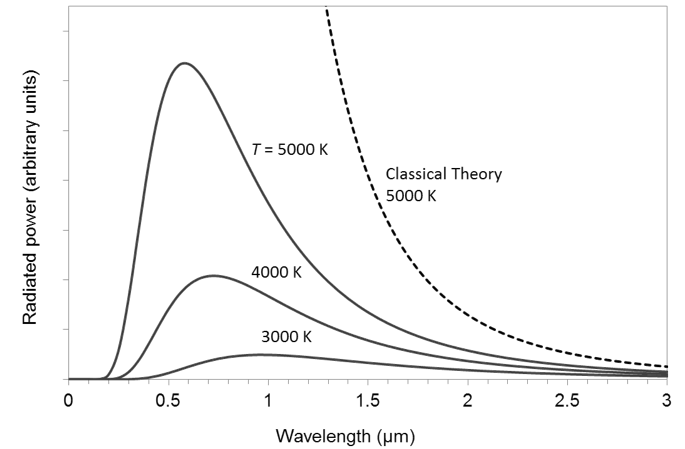
| (a) | Discuss how Max Planck accounted for observed black body spectra. | 4 |
| (b) | Outline how spectra from discharge tubes support Planck’s hypothesis regarding black body radiation spectra. | 2 |
Question 31 (3 marks)
Spectra can be used to determine the properties of stars,
| (a) | Identify two properties of a star that can be determine from an analysis of its spectrum. | 1 |
| (b) | Describe how the black body spectrum of the Sun can be used to determine one of the properties identified in (a). | 2 |
Question 32 (7 marks)
Students set up an experiment to verify Einstein’s photon theory of light.
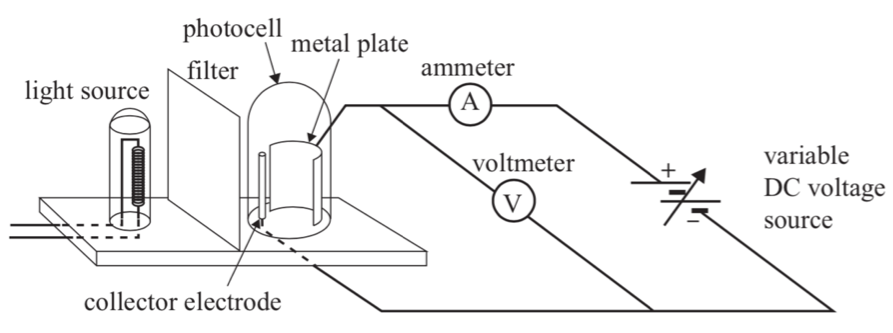
| (a) | Explain how the maximum kinetic energy of electrons ejected from the positive electrode is determined. | 3 |
| (b) | The Tungsten electrode is illuminated with light of frequency f , and stopping potential V_s is recorded for different values of f . Sketch a graph of V_s vs f that the students are expected to get.
| 1 |
| (c) | Outline how Planck’s constant and work function can be determined from the graph of V_s vs f . | 2 |
| (d) | The work function of tungsten is 4.5 \ eV . Calculate the threshold frequency of tungsten. | 1 |
Question 33 (8 marks)
wo inertial observers, A and B, agree to compare their measurements of time. They each carry an accurate clock.
During the experiment, A observes B to be moving at a constant velocity, v , as shown below.
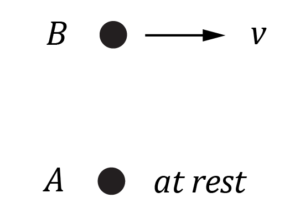
A and B observe two events.
| (a) | For the first event, B measured a proper time of 12 seconds while A measured 20 seconds. Calculate the speed of B as measured by A. | 1 |
| (b) | The second event is at rest with respect to observer A. Observer B measures 12 seconds for this event. Calculate the time interval of the second event as measured by A. | 2 |
| (c) | Which version of time is correct in each event? Explain your answer. | 2 |
| (d) | Outline experimental evidence that validated the prediction of time dilation. You may use a diagram to aid your answer. | 3 |
Question 34 (8 marks)
The muon is an elementary particle that can travel at relativistic speeds. The mass of the muon as a function of its speed is shown in the graph below.
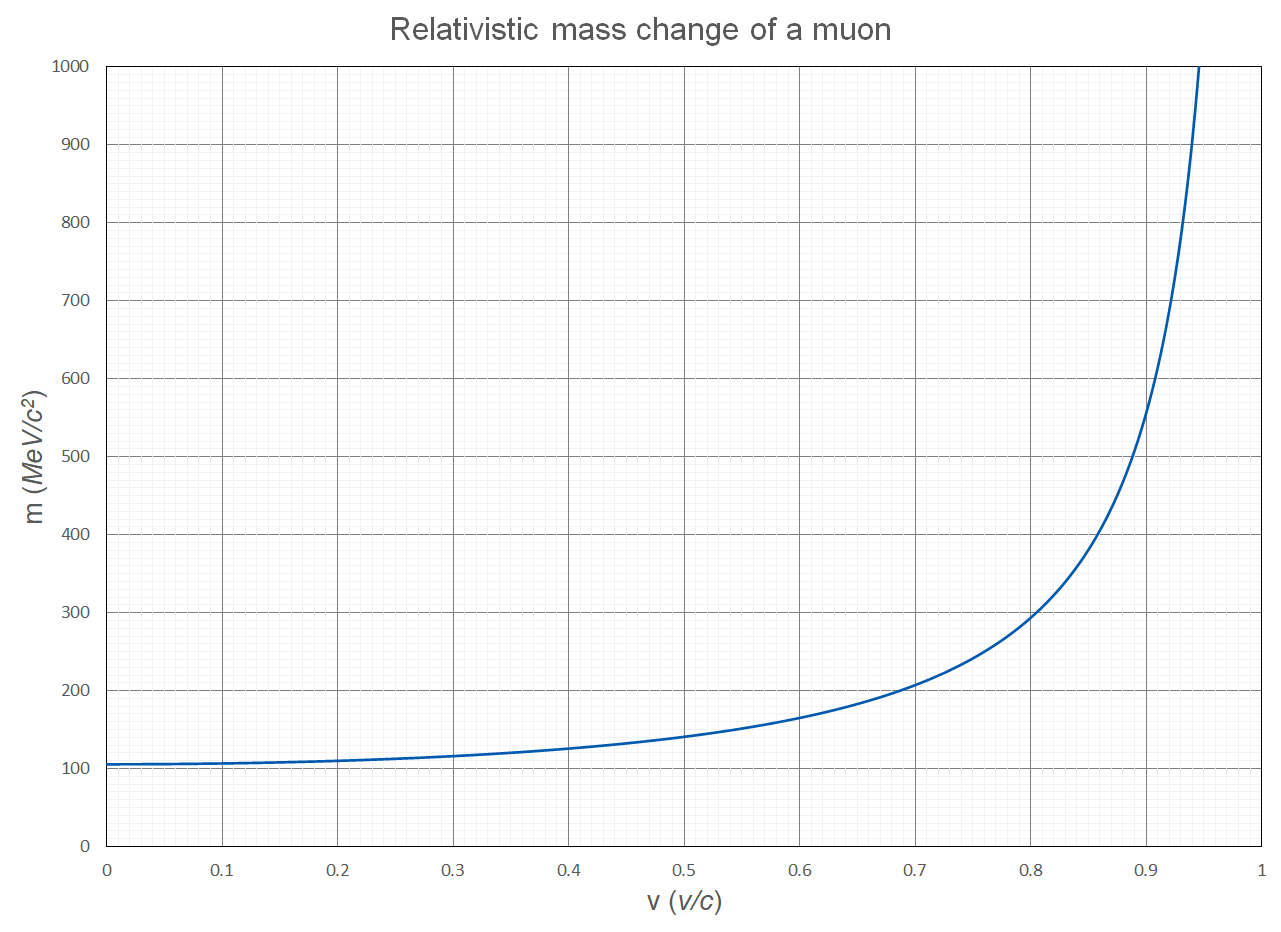
| (a) | What is the rest mass of the muon in kg? | 1 |
| (b) | Determine the speed at which the muon must travel in order to have a mass three times its rest mass. | 2 |
| (c) | Can the muon reach a speed faster than the speed of light by applying a constant net external force? Explain. | 2 |
| (d) | Muons and anti-muons are anti-particles of each other. When a muon combines with an anti-muon, both are annihilated and two gamma photons are produced. Calculate the wavelength of radiation carried by each photon using the rest mass of a single muon as determined in part (a). | 3 |
Question 35 (4 marks)
A portable hand-held vacuum cleaner is powered by a brushed DC electric motor and a 25 V battery.
The vacuum cleaner is tested in two different ways to determine its operational efficiency.
- Test 1: The vacuum cleaner is operated continuously without stopping.
- Test 2: The vacuum cleaner is started and stopped frequently.
The results of the tests are shown in the table below:
| Test 1 | Test 2 | |
| Duration of operation (minutes) | 60 | 30 |
| (a) | Explain why the vacuum cleaner operated for longer duration in Test 1. | 3 |
| (b) | Sketch a graph of net EMF vs speed for Test 1.
| 1 |
End of Exam Paper
See detailed solutions to the Mock HSC Physics Trial Exam Paper by creating your free account
Detailed step-by-step solutions for the Mock Physics Trial Exam Paper are available on Learnable. Please login or create your free account to access the complete solutions.

Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.