In this article
Module 1 'Kinematics' Practice Test | Year 11 Physics
Can you solve these 9 Kinematics practice questions? Test your exam-readiness with our Module 1 'Kinematics' Practice Test.
Practice Test for Year 11 Physics Module 1 ‘Kinematics’
The most effective way to finalise your exam preparation for Physics is to attempt as many exam-style questions as possible.
In this article, we’ve compiled 9 must-know questions on Module 1 ‘Kinematics’ to assist you with your exam preparation.
Module 1 ‘Kinematics’ assesses your fundamental knowledge in Physics, including vector operations and characteristics of motion.
Year 11 Physics Module 1 ‘Kinematics’ Physics Practice Test covers topics on:
- Vector Operations in Two Dimensions
- Analysing One-Dimensional Motion
- Graphing One-Dimensional Motion
- Relative Velocity
- Equations for Straight-Line Motion
- Change in Velocity and Acceleration
- Two-Dimensional Relative Velocity
- Two-Dimensional Resultant Velocity
Related: Looking for Year 11 Physics Module 2 ‘ Dynamics’ Practice Test?
Year 11 Physics Module 1 ‘Kinematics’ Practice Test
Instructions
General instructions for sitting the Module 1 ‘Kinematics’ Practice Test are outlined below.
- Reading Time: 5 minutes
- Working Time: 50 minutes
- Total marks: 32 marks
- Write using black pen
- Draw diagrams using pencil
- Calculators approved by NESA may be used
- A formulae sheet, data sheet and periodic table can be used
- There are 9 questions, with marks ranging from 1 to 6 marks.
In the final HSC Physics Exam, you will have approximately 1.8 minutes per mark.
In practice exams, you should aim to answer questions at a pace of 1.5 minutes per mark.
To simulate real exam conditions:
- Put away your notes and other distractions in your study environment
- Close all unnecessary tabs and mute notifications on your device
- Set a timer for 55 minutes
- Complete this exam in a quiet environment where you will not be disturbed for the duration of the exam.
Question 1: Vector Operations in Two Dimensions
What is the result of subtracting 300 m South from 200 m East? (1 mark)
| (A) | 361 \ m \ N41.8 \degree E |
| (B) | 361 \ m \ N 33.7 \degree E |
| (C) | 361 \ m \ S41.8 \degree W |
| (D) | 361 \ m \ S33.7 \degree W |
Question 2: Scalars and Vectors
Explain the difference between a scalar and a vector with reference to distance and displacement. (2 marks)
See Question 2 Solution
Question 3: Analysing One-Dimensional Motion
The graph of velocity vs time for a car travelling in a straight line is shown below.
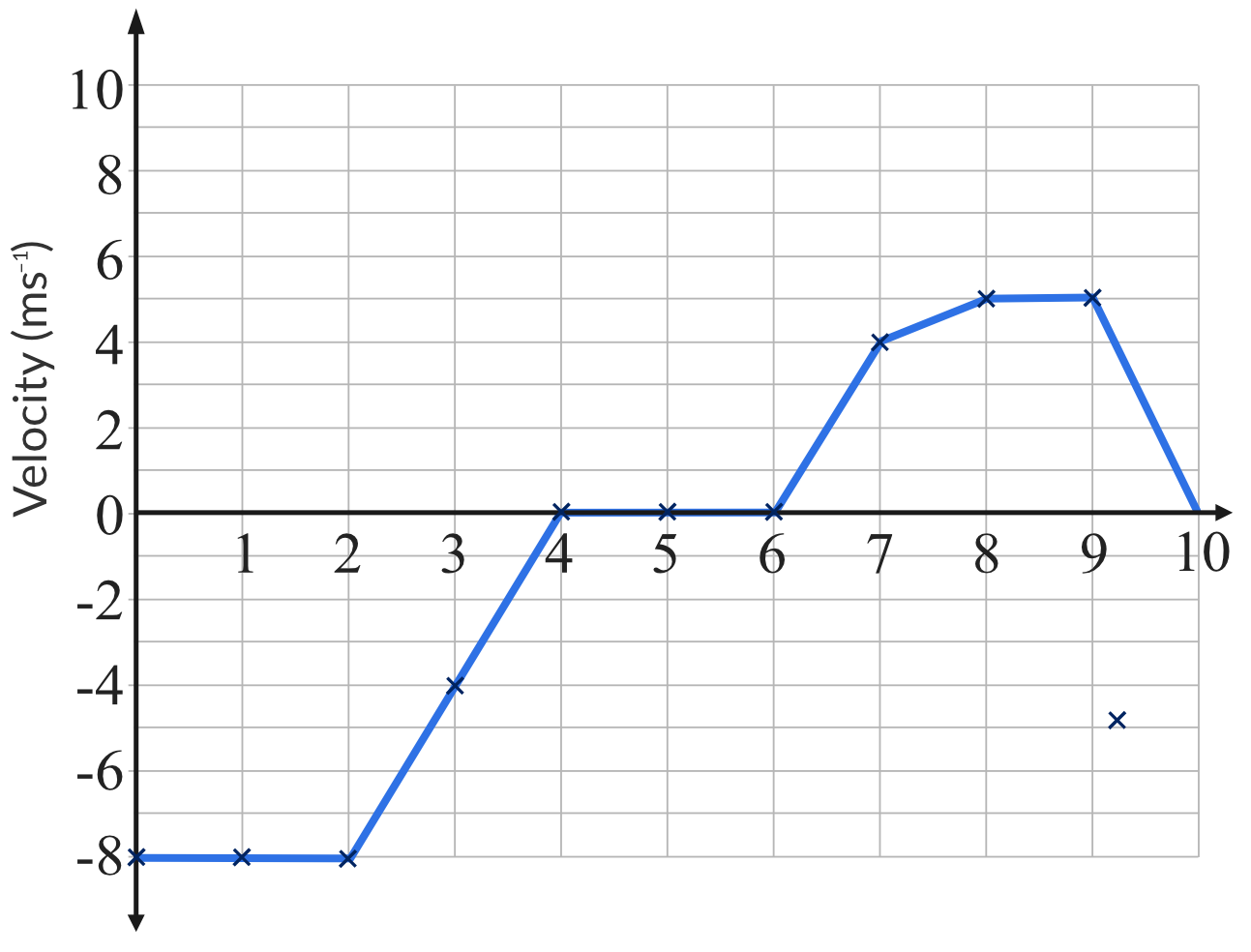
| (a) | Using the graph, find the acceleration and displacement of the car for the following time intervals:
| 3 | ||||||||||||||||||||||||
| (b) | What is the car’s total displacement at the end of the 10 s trip? | 1 | ||||||||||||||||||||||||
| (c) | Calculate the car’s average velocity. | 1 |
Question 4: Graphing One-Dimensional Motion.
A ball is thrown vertically upwards with an initial velocity of 19.6 ms^{-1} . The ball returns to its original position after 4 seconds.
| (a) | Sketch a graph of displacement vs time for the journey of the ball. Include relevant displacement values in the graph. | 2 |
| (b) | Sketch a graph of velocity vs tim for the journey of the ball. Include relevant velocity values in the graph. | 2 |
| (c) | Sketch a graph of acceleration vs time for the journey of the ball. Include relevant acceleration values in the graph. | 2 |
Question 5: Relative Velocity
Two trains A and B pass each other. Train A is travelling at 100 \ kmh^{-1} West and train B is travelling at 80 \ kmh^{-1} in the same direction. A passenger in Train A is running at 10 \ kmh^{-1} towards the back of the train.
| (a) | What is the velocity of train A relative to train B? | 2 |
| (b) | What is the velocity of train B relative to train A? | 2 |
| (c) | What is the velocity of the passenger in train A relative to the ground? | 2 |
Question 6: Equations for Straight-Line Motion
A metal ball is dropped from rest onto a large pile of foam from a height of 7 \ m above the foam. As the ball falls, it accelerates at 9.8 \ ms^{-2} downwards. The ball hits the foam and travels through it, penetrating to a depth of 8.5 \ m before it comes to a stop.
Calculate the acceleration of the ball in the foam (assume uniform acceleration) to two significant figure. (3 marks)
See Question 6 Solution
Question 7: Change in Velocity and Acceleration
A pinball in a pinball machine ricochets off a bumper. The collision occurs over 0.05 s.
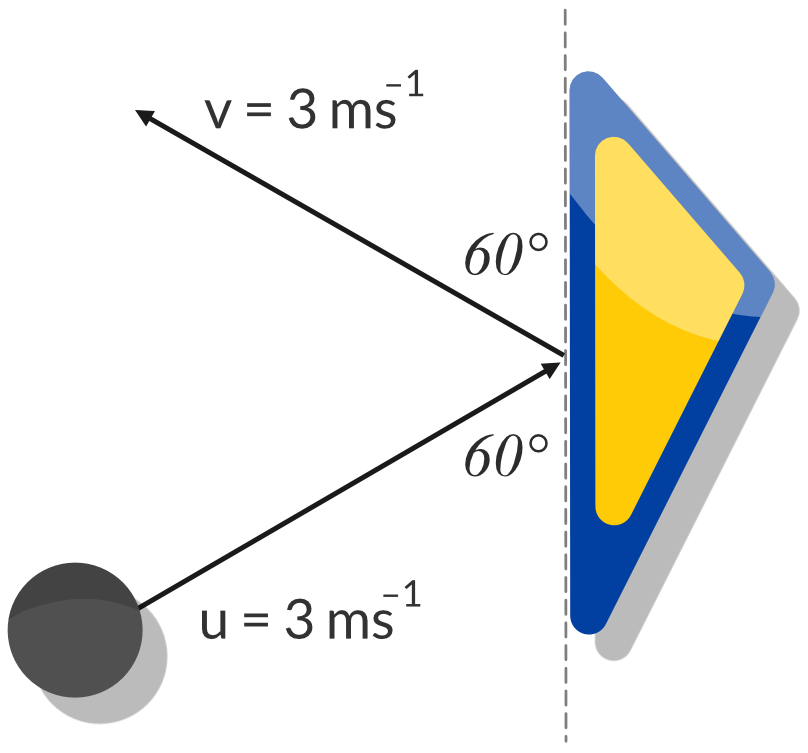
| (a) | Calculate the pinball’s change in velocity. | 3 |
| (b) | Calculate the magnitude of the pinball’s acceleration. | 1 |
Question 8: Two-Dimensional Relative Velocity
Aeroplane X flies with a velocity of 200 \ ms^{-1} \ North , while aeroplane Y flies at a velocity of 250 \ ms^{-1} \ East . Calculate the velocity of aeroplane X with respect to aeroplane Y. Express your answer to three significant figures. (3 marks)
See Question 8 Solution
Question 9: Two Dimensional Resultant Velocity
An aeroplane is travelling at velocity 200 \ ms^{-1} South with respect to the air.
| (a) | The aeroplane encounters a crosswind from the East at 40 \ ms^{-1} . Find the velocity of the plane relative to the ground, expressing your answer to three significant figures. | 2 |
| (b) | If the pilot wishes to reach a point due South of his starting point, in what direction should the pilot fly the aeroplane? | 2 |
| (c) | Calculate the magnitude of the velocity of the aeroplane relative to the ground in part (b). Express your answer to three significant figures. | 1 |
Solutions for Year 11 Physics Module 1 ‘Kinematics’ Practice Test
The solutions for the Module 1 ‘Kinematics’ Practice Test is more detailed than the required marking guidelines to help students with mark their test easily.
Once you have completed the Module 1 ‘Kinematics’ Practice Test, mark each question carefully using the provided solutions and note any areas for improvement.
Marking practice exams is just as important as answering the questions.
Question 1 solution
Constructing a vector diagram is the most efficient away to answer these question types. Now note that this subtraction is equivalent to:
{(300 \ m \ South) + ( - 200 \ m \ East) = (300 \ m \ South) + ( 200 \ m \ West)} .
The negative sign reverses the direction of the vector, so the 200 \ m vector becomes directed towards the West. This turns the question into a vector addition problem.
By then drawing a vector diagram using the data provided in the question, and the information above, we can construct the resultant vector.
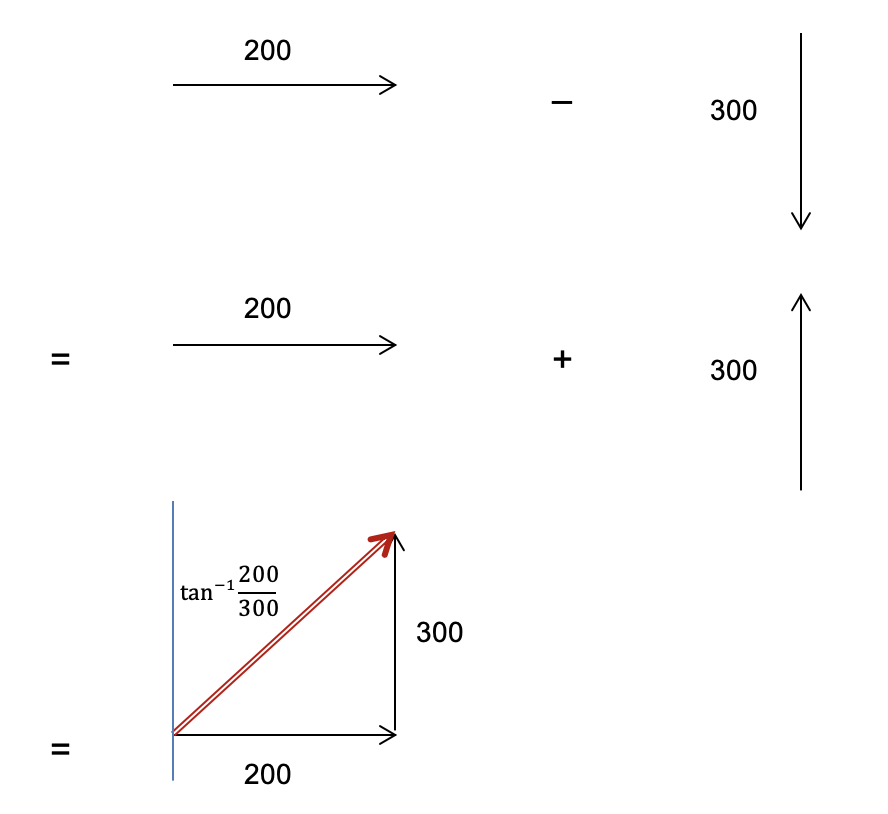
From the vector diagram, we can use trigonometry to calculate the magnitude and direction of the resultant vector.
Magnitude:
{\sqrt{200^2 + 300^2} = 360.555... = 361 \ m}
Direction:
\theta = tan^{-1} \bigg( \frac{200}{300} \bigg) = 33.7 \degree
Therefore, the resultant vector is 361 \ m \ N33.7 \degree E
Answer: (B)
Question 2 solution
Distance is the length of the path travelled by an object and is a scalar quantity whereas displacement is the change in position of an object and is a vector quantity.
Distance only requires the magnitude whereas displacement requires both the magnitude and the direction when describing it.
Question 3 solution
Part (a)
In a velocity vs time graph:
- \vec{a} = Gradient of the graph
- \Delta \vec{s} = Area under the graph
Hence,
| Time interval (s) | Acceleration (ms^{-2}) | Displacement (m) |
| 0-2 | 0 | -16 |
| 2-4 | 4 | -8 |
| 4-6 | 0 | 0 |
| 6-7 | 4 | 2 |
| 7-8 | 1 | 4.5 |
| 8-9 | 0 | 5 |
| 9-10 | -5 | 2.5 |
Part (b)
The total displacement of the car can be calculated by adding the displacement of the car in each time interval:
\vec{s} = -16 - 8 + 0 + 2 + 4.5 + 5 + 2.5 = -10 \ m
Answer: -10 \ m
Part (c)
The car’s average velocity can be found through the formula:
{ \vec{v} = \dfrac{\Delta \vec{s}}{t} = \dfrac{-10}{10} = -1 \ ms^{-1} }
Answer: -1 \ ms^{-1}
Question 4 solution
Part (a)
Calculate the maximum height the ball reaches.
\begin{aligned} v^2&=u^2+2as\\ 0&= 19.6^2+2(-9.8)s \\ s&=19.6 m \end{aligned}
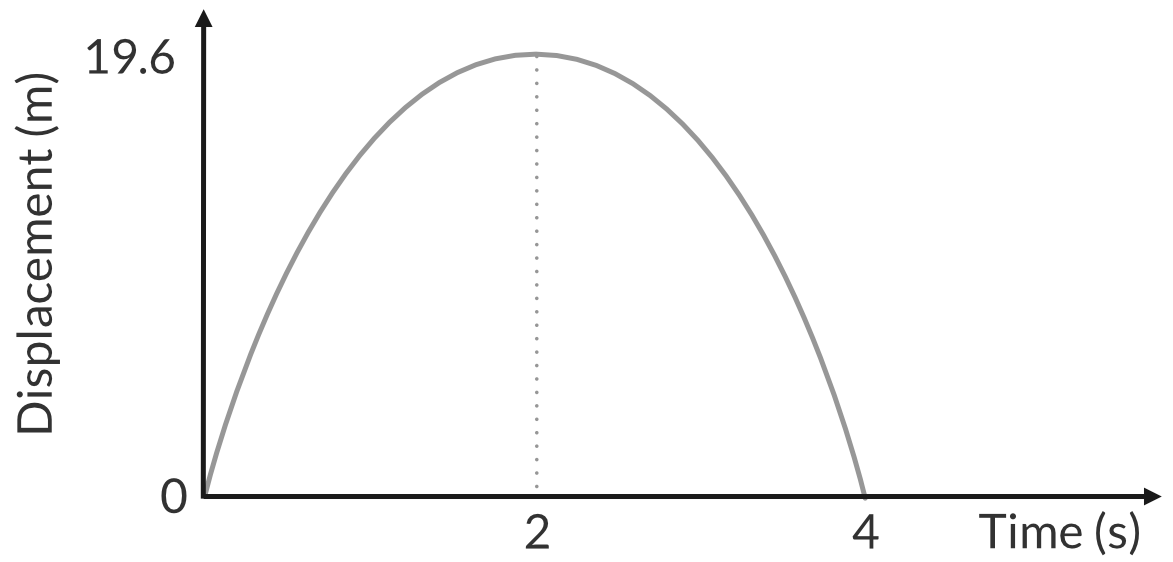
Part (b)
The velocity of the decreases on its way and increases on its way at 9.8 ms^{-2}.
- The initial velocity of the ball is 19.6 m/s upwards.
- At the maximum height the velocity is zero.
- The final velocity of the ball is 19.6 m/s downwards
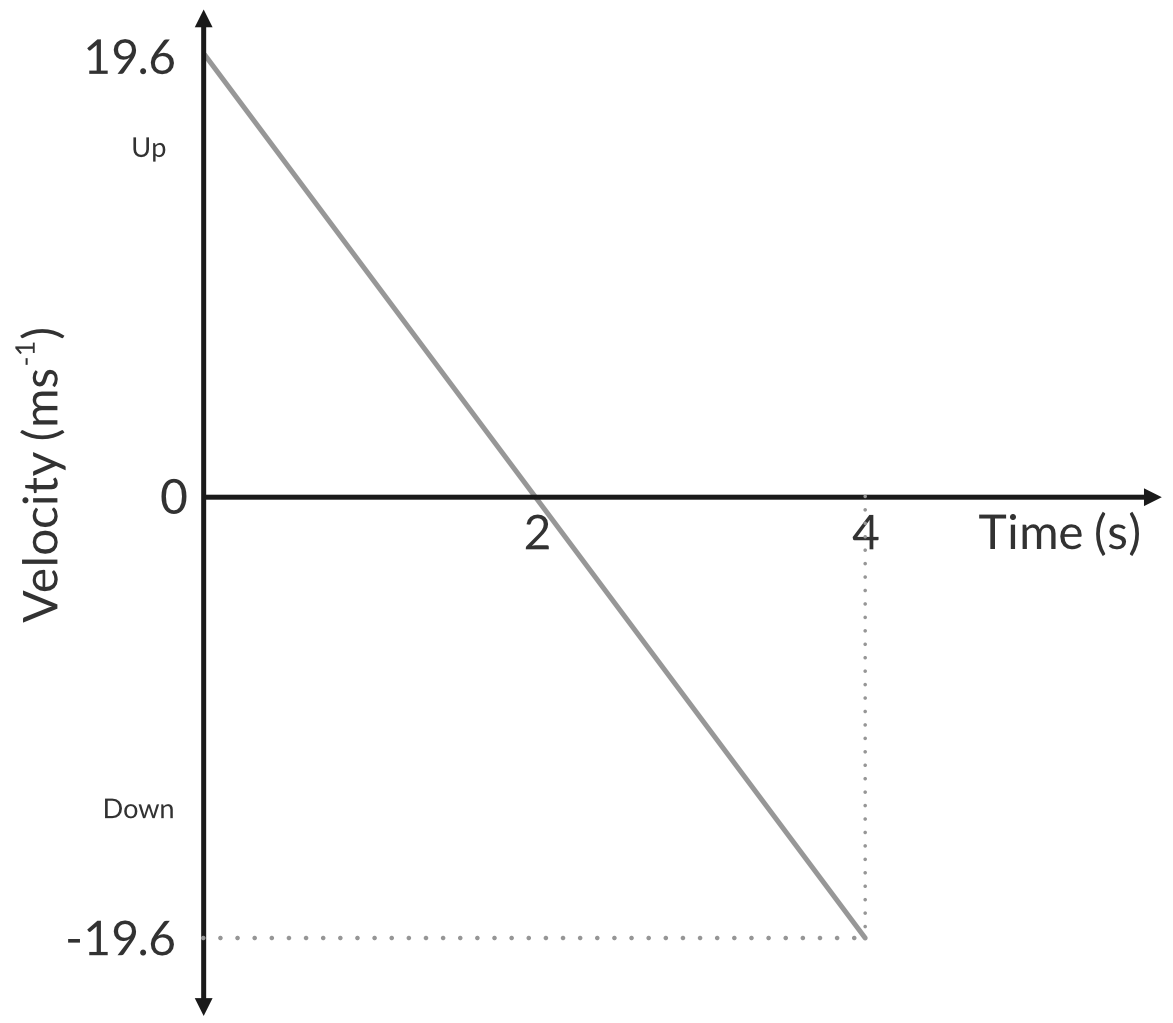
Part (c)
The acceleration fo the ball is constant, 9.8 ms^{-2}.
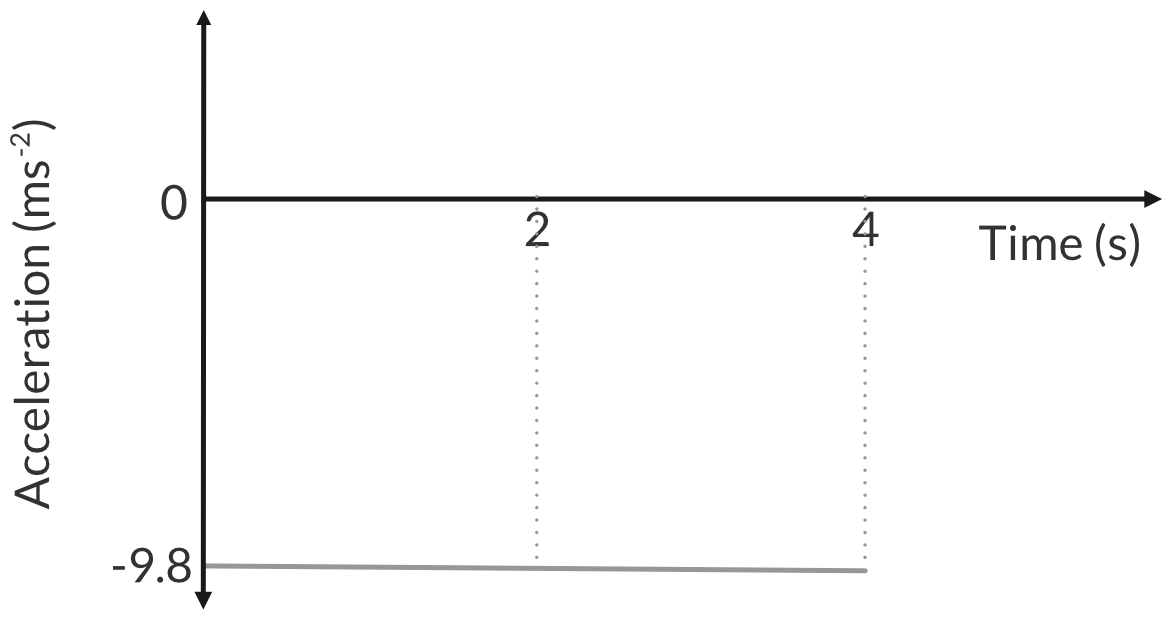
Question 5 solution
Part (a)
Recall that relative velocity is given by v_{AB} = v_{AG} - v_{BG} , where:
- v_{AB} is the velocity of train A relative to train B
- v_{AG} is the velocity of train A relative to the ground
- v_{BG} is the velocity of train B relative to the ground
Therefore, taking west as the positive direction:
v_{AB} = 100 - 80 = 20 \ kmh^{-1} \ West
Answer: 20 \ kmh^{-1} \ West
Part (b)
Similarly, the velocity of train B relative to train A is given by {v_{BA} = v_{BG} - v_{AG}} ,
where:
- v_{BA} is the velocity of train B relative to train A
- v_{BG} is the velocity of train B relative to the ground
- v_{AG} is the velocity of train A relative to the ground
Therefore, taking west as the positive direction:
v_{AB} = 80 - 100 = -20 \ kmh^{-1} = 20 \ kmh^{-1} \ East
Answer: 20 \ kmh^{-1} \ East
Part (c)
The velocity of the passenger in train A relative to the ground is given by v_{PG} = v_{PA} + v_{AG}
- v_{PG} is the velocity of the passenger relative to the ground
- v_{PA} is the velocity of the passenger relative to train A
- v_{AG} is the velocity of train A relative to the ground
Therefore, taking West as the positive direction:
v_{PG} = -10 + 100 = 90 \ kmh^{-1} \ West
Answer: 90 \ kmh^{-1} \ West
Question 6 solution
Step 1: Find the velocity of the ball just before impact with the foam.
Identify the given data in SI units. In order to use the equation of the motion, you require 3 of the 4 variables to solve the unknown.
- \vec{s}_1 = 7 \ m
- \vec{a} = 9.8 \ ms^{-2}
- \vec{u} = 0
- \vec{v} = ?
Calculate the ball’s velocity when it reaches the foam
\begin{aligned} \vec{v}^2 &= \vec{u}^2 + 2 \vec{a} \vec{s} \\\\ &= 0 + 2 (9.8 \times 7) \\\\ \therefore \vec{v} &= \sqrt{137.2} \end{aligned}
Step 2: Using the final velocity in Step 1, calculate the acceleration of the ball in the foam.
The ball enters the foam and travels through the foam until it stops. Hence, in this case:
- \vec{u} = \sqrt{137.2} \ ms^{-1}
- \vec{v} = 0
- \vec{s}_2 = 8.5 \ m
\begin{aligned} \vec{v}^2 &= \vec{u}^2 + 2 \vec{a} \vec{s} \\\\ 0 &= 137.2 + 17 \vec{a} \\\\ \therefore \vec{a} &= - \dfrac{137.2}{17} \\\\ \vec{a} &= - 8.0705... \end{aligned}
Answer: \vec{a} = - 8.1 \ ms^{-2} (2 s.f.)
Question 7 solution
The vector diagram representing the relationship between the initial velocity, final velocity and change in velocity is shown below.
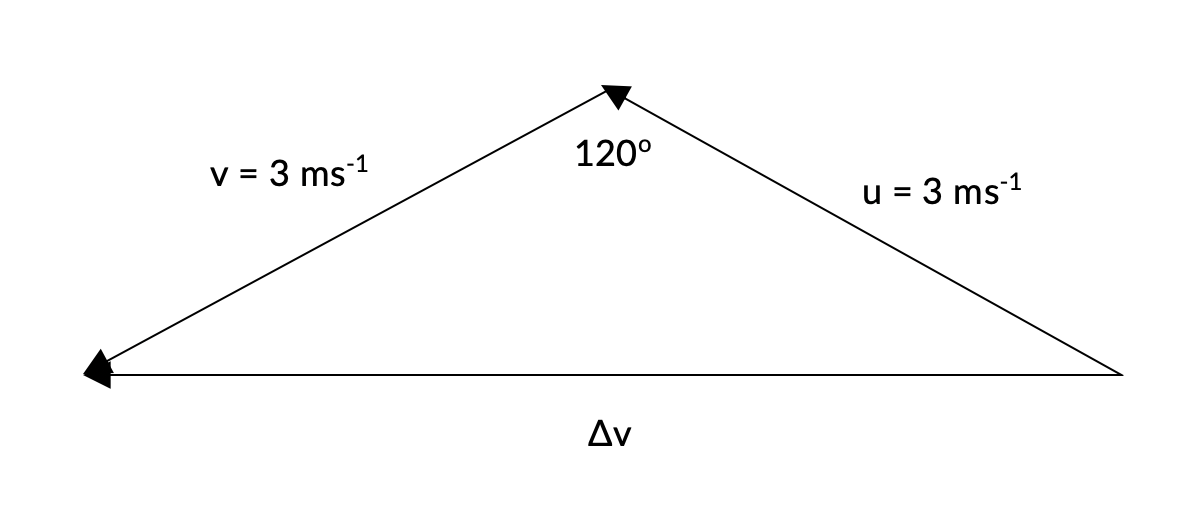
Using the cosine rule, we can calculate the magnitude of the change in velocity.
\begin{aligned} (\Delta \vec{v} )^2 &= \vec{u}^2 + \vec{v}^2 - 2 \vec{u} \vec{v} cos 120 \degree \\\\ (\Delta \vec{v} )^2 &= 3^2 + 3^2 - 2 (3)(3) cos 120 \degree \\\\ \therefore (\Delta \vec{v} )^2 &= 5.2 \ ms^{-1} \ (2 \ s.f.) \end{aligned}
The direction of the change in velocity vector is to the left.
Answer: 5.2 \ ms^{-1} to the left
Part (b)
The acceleration is calculated using the formula \vec{a} = \dfrac{ \Delta \vec{v}}{ \Delta t} . The question tells us that the collision occurs over 0.05 seconds, and we calculated the change in velocity in part a).
\begin{aligned} \therefore \vec{a} &= \dfrac{ 5.2 \ ms^{-1} \ left}{0.05 \ s} \\\\ \vec{a} &= 103.9 \ ms^{-2} \ left \\\\ \vec{a} &= 104 \ ms^{-2} \ left \ (3 \ s.f.) \end{aligned}
Answer: \vec{a} = 104 \ ms^{-2} \ left
Question 8 solution
Step 1: Draw a vector diagram using the information provided.
Our vector diagram should show the relationship between the two known variables:
- The velocity of aeroplane X relative to the ground (\vec{v}_{XG})
- The velocity of aeroplane Y relative to the ground (\vec{v}_{YG})
It should also include the variable we are required to solve for:
- The velocity of aeroplane X relative to aeroplane Y (\vec{v}_{XY})
We additionally know that \vec{v}_{XY} = \vec{v}_{XG} - \vec{v}_{YG}
Using this relationship, we can construct our vector diagram:
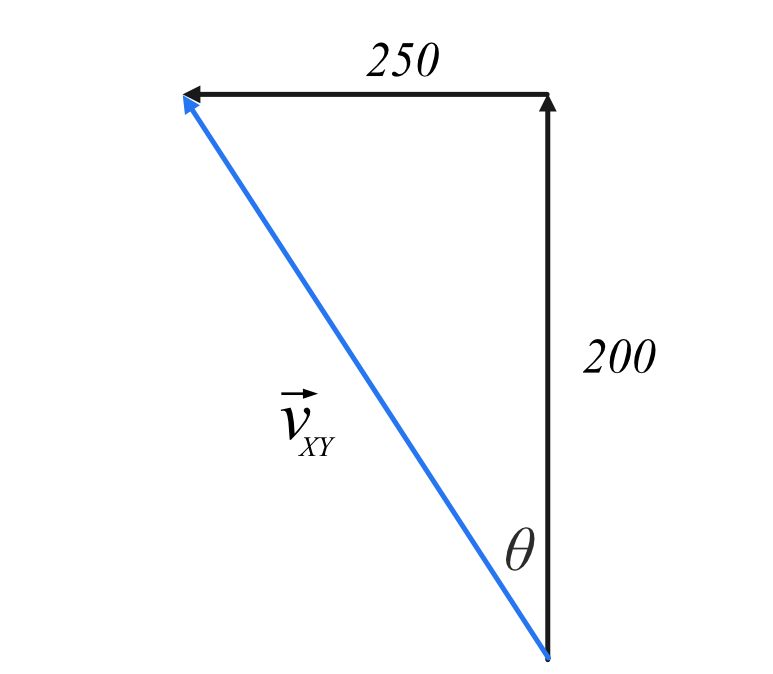
Step 2: Use Pythagoras’ Theorem to calculate the magnitude of \vec{v}_{XY}
\begin{aligned} \vec{v}_{XY} &= \sqrt{(200)^2 + (250^2)} \\\\ &= 320.156... \\\\ &= 320 \ ms^{-1} \ (3 \ sig. \ fig) \end{aligned}
Step 3: Calculate the direction of \vec{v}_{XY} using trigonometry.
\begin{aligned} tan \theta &= \frac{opposite}{adjacent} \\\\ &= \frac{250}{200} \\\\ \therefore \theta &= tan^{-1}(\frac{5}{4}) \\\\ &= 51.3401... \\\\ &= 51.3 \degree \ (3 \ sig. \ fig) \end{aligned}
By analysing the vector diagram, we can see that the velocity is in the direction of North-West.
Answer: The velocity of aeroplane X relative to aeroplane Y is 320 \ ms^{-1} \ N 51 \degree W
Question 9 solution
Part (a)
Step 1: Draw a vector diagram using the data provided.
Our vector diagram should show the relationship between the two known variables:
- The velocity of the aeroplane relative to the wind ( \vec{v}_{PW} )
- The velocity of the wind relative to the ground ( \vec{v}_{WG} )
It should also include the variable we are required to solve for:
- The velocity of the plane relative to the ground ( \vec{v}_{PG} )
We additionally know that \vec{v}_{PG} = \vec{v}_{WG} + \vec{v}_{PW}
Hence, we can construct a vector diagram:
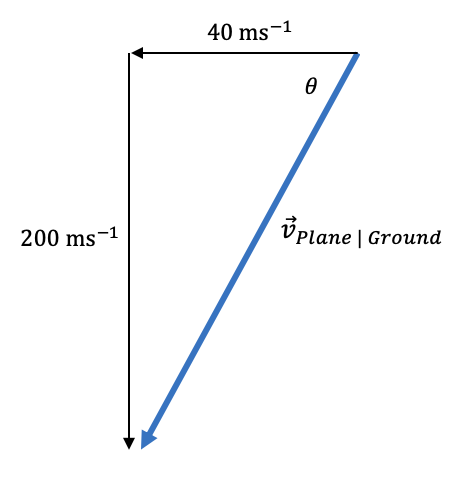
It is important to note that the wind is from the East. This means it travels Westward.
Step 2: Use Pythagoras’ Theorem to determine the magnitude of the plane’s velocity relative to the ground.
\begin{aligned} \vec{v}_{PG} &= \sqrt{(40^2) + (200)^2} \\\\ &= 203.960... \\\\ &= 204 \ ms^{-1} \ (3 \ sig. \ fig) \end{aligned}
Step 3: Use trigonometry to determine the direction of the plane’s velocity relative to the ground.
\begin{aligned} tan\theta &=\frac{opposite}{adjacent} \\\\ &= \frac{40}{200} \\\\ \therefore \theta &=tan^{-1} \bigg( \frac{40}{200} \bigg) \\\\ &= 11.30993... \\\\ &= 11.3 \degree \end{aligned}
By analysing our diagram, we can see that the direction of this velocity is South-West.
Answer: The velocity of the plane relative to the ground is 204 \ ms^{-1} \ S11.3 \degree W .
Part (b)
Step 1: Draw a vector diagram using the data provided.
Similar to Part (a), our vector diagram must derive the relationship between \vec{v}_{PW}, \vec{v}_{WG} and \vec{v}_{PG} . However, this vector diagram must derive the relationship required in order for the plane to fly South:
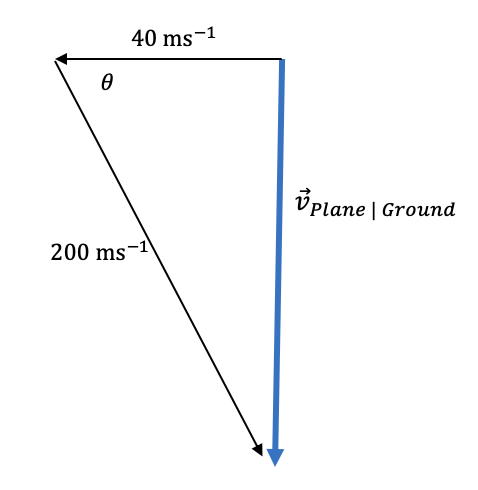
Step 2: Use trigonometry to calculate the direction the pilot must fly the aeroplane.
In this scenario, we use cos \theta = \frac{adjacent}{hypotenuse} to determine the angle.
\begin{aligned} cos \theta &= \frac{40}{200} \\\\ \theta &= cos^{-1} \bigg( \frac{40}{200} \bigg) \\\\ &= 78.463... \degree \\\\ &= 78.5 \degree \end{aligned}
Step 3: State the direction using compass bearing.
(90 - 78.5) = S11.5 \degree E
Answer: The plane’s velocity relative to the ground will be South if it travels in the direction S 11.5 \degree E
Part (c)
Use Pythagoras’ Theorem to calculate the velocity of the plane relative to the ground:
\begin{aligned} \vec{v}_{PG} &= \sqrt{200^2 - 40^2} \\\\ &= 195.950... \\\\ &= 196 \ ms^{-1} \ (3 \ sig. \ fig) \end{aligned}
Answer: 196 \ ms^{-1}
Back to the Module 1 ‘Kinematics’ Practice Test.
Want more practice questions on Module 1 ‘Kinematics’?
Test your depth of understanding on any Module 1 ‘Kinematics’ concept in just 10 minutes with Learnable’s customisable quiz builder with over 500+ questions from each module. Instant feedback provides immediate adjustments on your misconceptions. Try Learnable for free now.
Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.