In this article
Module 2 'Dynamics' Practice Test | Year 11 Physics
Looking for Module 2 'Dynamics' practice exam questions? Get exam ready for your Physics half-yearly exam with our Module 2 'Dynamics' Practice Test.
Practice Test for Year 11 Physics Module 2 ‘Dynamics’
Do you have a half-yearly exam on Year 11 Physics Module 2 Dynamics?
We’ve compiled 10 must-know exam-style questions on Year 11 Physics Module 2 ‘Dynamics’ that will help you ace your half-yearly exam.
Module 2 ‘Dynamics’ assesses the fundamental laws in physics including Newton’s Laws and is considered the most important Year 11 Physics Module.
Module 2 ‘Dynamics’ Physics Practice Test covers topics on:
- Newton’s Laws
- Forces on Single Bodies
- Analysing Forces in Two Dimensions
- Analysing Forces on Inclined Slopes
- Static Friction
- Energy and Work
- Impulse-Time Graphs
- Momentum and Impulse
- Collisions
Related: Looking for Year 11 Physics Module 1 ‘Kinematics Practice Test?
Year 11 Physics Module 2 ‘Dynamics’ Practice Test
Instructions
General instructions for sitting the Module 2 ‘Dynamics’ Practice Test are outlined below.
- Reading Time: 5 minutes
- Working Time: 55 minutes
- Total marks: 31 marks
- Write using black pen
- Draw diagrams using pencil
- Calculators approved by NESA may be used
- A formulae sheet, data sheet and periodic table can be used
- There are 10 questions, with marks ranging from 1 to 5 marks.
In the final HSC Physics Exam, you will have approximately 1.8 minutes per mark.
In practice exams, you should aim to answer questions at a pace of 1.5 minutes per mark.
To simulate real exam conditions:
- Put away your notes and other distractions in your study environment
- Close all unnecessary tabs and mute notifications on your device
- Set a timer for 55 minutes
- Complete this exam in a quiet environment where you will not be disturbed for the duration of the exam.
Once you have completed the Module 2 ‘Dynamics’ practice exam, mark each question carefully using the provided solutions and note any areas for improvement.
Marking practice exams is just as important as answering the questions.
Question 1: Newton’s Laws
A 2400 kg car accelerates uniformly from 10 \ ms^{-1} to 30 \ ms^{-1} in 6 seconds.
What is the net external force acting on the car? (1 mark)
| (A) | 816 N |
| (B) | 8000 N |
| (C) | 12 000 N |
| (D) | 78 4000 N |
Question 2: Newton’s Laws
A car is speeding along the road in the snowy mountains and comes to an icy bend. As the driver tries to turn the car, it slides straight ahead and off the road.
Explain why the car failed to turn the corner, with reference to the relevant Newtonian Law of motion. (3 marks)
Question 3: Forces on Single Bodies
A car of mass 540 kg was accelerated along a flat road, from rest to 15 \ ms^{-1} in 7.5 seconds.
| (a) | What was the car’s acceleration? | 1 |
| (b) | What was the net external force acting on the car? | 1 |
| (c) | The driving force from the car’s engine was 1600 N. If the only other force acting was the friction of the road, what was the magnitude of that friction force? | 2 |
Question 4: Analysing Forces in Two Dimensions
A car is moving down a 5 \degree slope at a constant velocity. The frictional forces acting against the car are equal to 1000 N.
| (a) | Draw a diagram showing all the forces acting on the car. Label the forces clearly. | 1 |
| (b) | Determine the net force acting on the vehicle along the inclined plane. | 1 |
| (c) | Determine the mass of the car. Express your answer to four significant figures. | 2 |
Question 5: Analysing Forces in Pulley Systems.
Two blocks, 2 kg and 4 kg are on double inclined slopes as shown below.

| (a) | Calculate the acceleration of the blocks. Express your answer to two significant figures. | 2 |
| (b) | Hence, or otherwise, calculate the tension in the string. | 2 |
Question 6: Static Friction
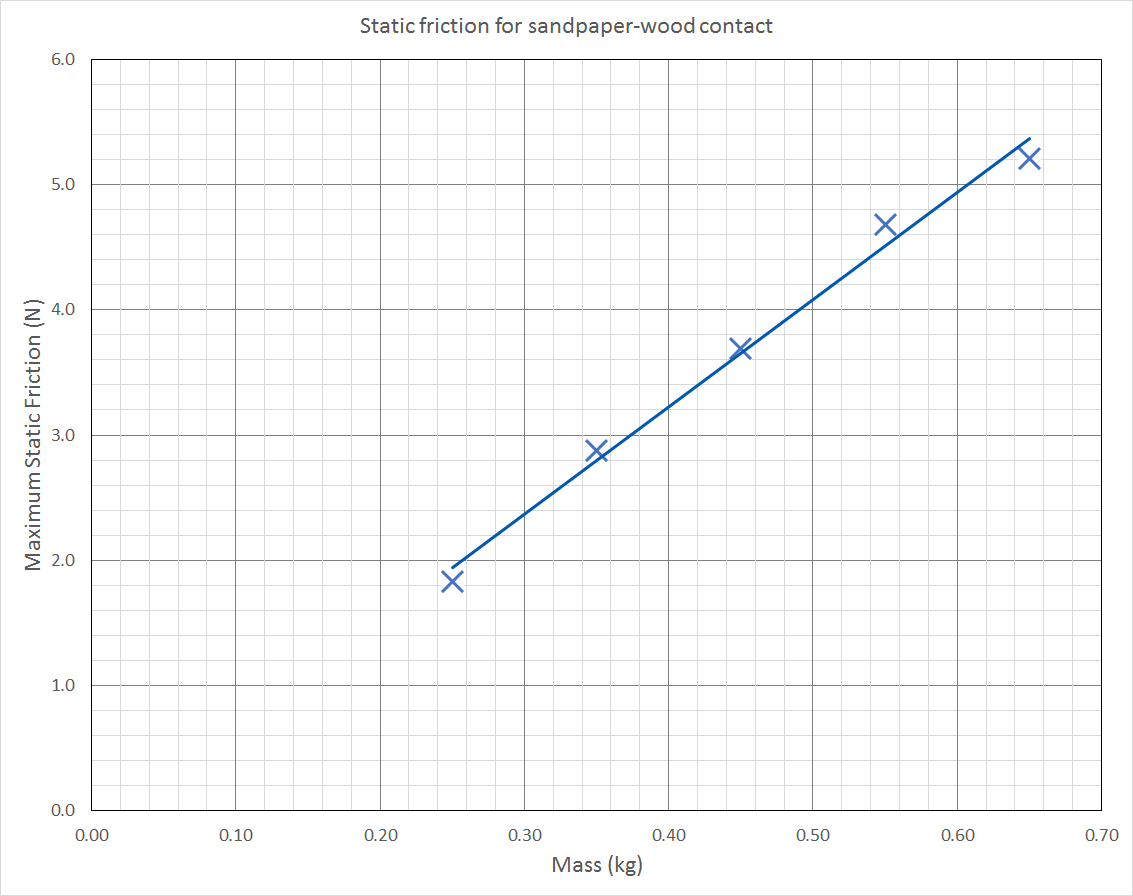
Madison conducts an experiment to calculate the coefficient of static friction between contact surfaces – sandpaper and wood. She sets up her experiment as shown in the diagram below.
The mass of the wooden block with sandpaper glued to one side was 0.25 kg.
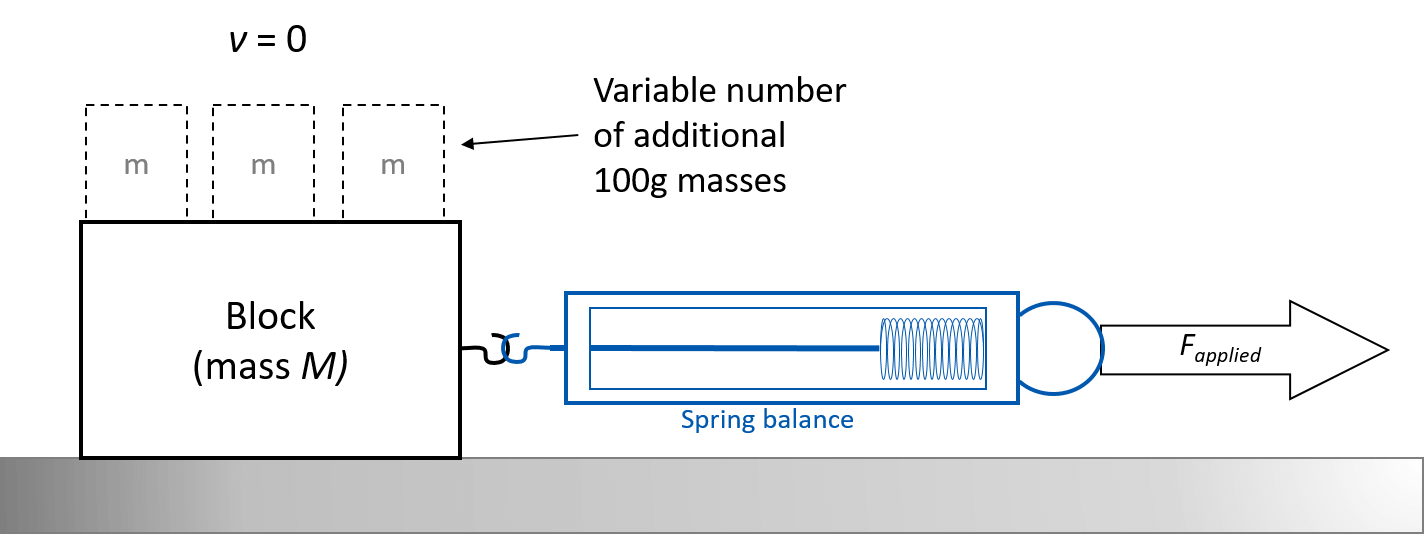
She pulled the spring balance horizontally until the wooden block slipped, and recorded the spring balance force reading at the moment this occurred. She then added 1, 2, 3 and 4 additional 100 gram masses on top of the block, recording 3 trials for each mass. Her results are shown below.
| Mass (kg) | Applied Force (N) trial 1 | Applied Force (N) trial 2 | Applied Force (N) trial 3 |
| 0.25 | 1.6 | 2.0 | 2.0 |
| 0.35 | 3.2 | 3.4 | 2.0 |
| 0.45 | 3.3 | 3.8 | 4.0 |
| 0.55 | 4.3 | 4.8 | 5.0 |
| 0.65 | 5.0 | 6.3 | 4.3 |
| (a) | Plot a graph of maximum static friction vs mass | 2 |
| (b) | Determine the significance of the gradient. | 2 |
| (c) | Hence or otherwise, determine the coefficient of static friction for the sandpaper-wood surface. (4 marks) | 2 |
Question 7: Energy and Work
Floyd pulls a 60 kg tyre with a force of 250 N at an elevation of 20 degrees to the horizontal.
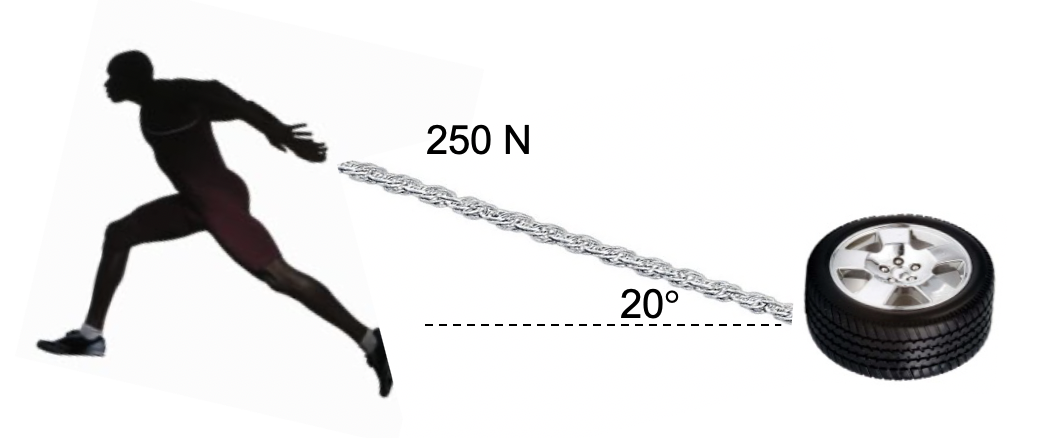
| (a) | If he is able to pull for 25 metres, calculate the work done by Floyd. Express your answer to two significant figures. | 2 |
| (b) | Provided that the tyre was initially at rest, calculate the velocity of the tyre if it reaches the 25 m mark. There is an additional frictional force of 220 N. Express your answer to two significant figures. | 2 |
Question 8: Impulse-Time Graphs.
A car travelling at 30 \ ms^{-1} comes to a stop. The time taken for the car to come to a stop \Delta t can vary. How does the average force that the car experiences change as a function of the time taken for the car to come to a stop?
| (A) | 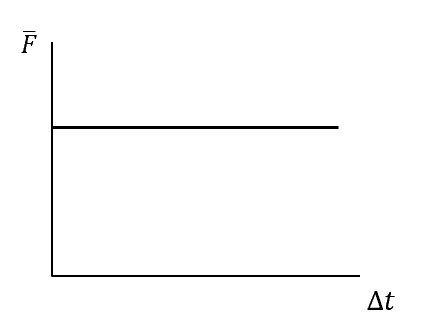 |
| (B) | 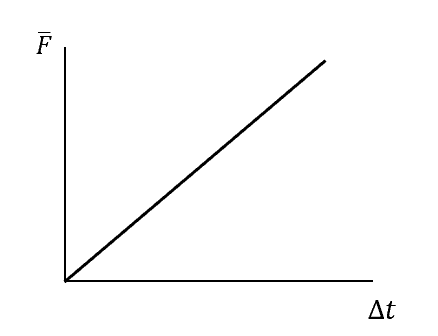 |
| (C) | 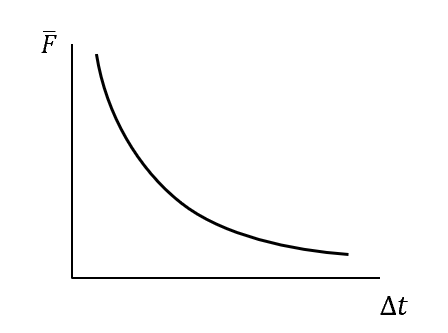 |
| (D) | 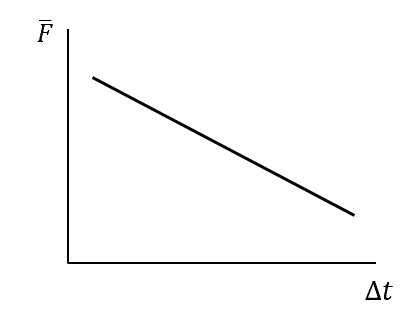 |
Question 9: Momentum and Impulse
Calculate:
| (a) | The momentum of a 500 g ball, which had an initial downward speed of 2 \ ms^{-1} , and has fallen through a height of 10 m to hit the ground. | 2 |
| (b) | The impulse of a 5 kg mass that undergoes an acceleration of 6 \ ms^{-2} over 3 seconds. | 2 |
Question 10: Collisions
Consider a collision between a 1500 kg car travelling at 16 \ ms^{-1} \ East , and a small truck of mass 2500 kg travelling at 20 \ ms^{-1} \ North .
| a) | What is the initial momentum of the car? | 1 |
| b) | What is the initial momentum of the truck? | 1 |
| c) | If the car and truck join together as a result of the collision, what is their final velocity? Be sure to include both magnitude and direction. Express your answer to three significant figures. | 2 |
Solutions for Year 11 Physics Module 2 ‘Dynamics’ Practice Test
The solutions for the Module 2 ‘Dynamics’ Practice Test is presented in a step-by-step manner and should be closely followed by students to maximise their marks in the exam.
Question 1 solution
Step 1: Identify the given data in SI units.
- m = 2400 \ kg
- \vec{u} = 10 \ ms^{-1}
- \vec{v} = 30 \ ms^{-1}
- t = 6 \ s
Step 2: Calculate the acceleration of the car.
\begin{aligned} a &= \dfrac{v-u}{t} \\ &= \dfrac{30-10}{6} \\ &= \dfrac{20}{6} \ ms^{-2} \end{aligned}
Step 3: Calculate the net external force acting on the car using the formula Fnet = ma
\begin{aligned} F_{net} &= ma \\ &= 2400 \times \dfrac{20}{6} \\ &= 8000 \ N \end{aligned}
Answer: (B)
Question 2 solution
When answering ‘explain’ questions students should use Learnable’s CEO Framework TM (Cause, Effect, Outcome) to construct a logical and sequential answer.
| CEO Framework | Detail |
| Cause | Newton’s first law states that an object will continue in its state of motion unless acted upon by an external force. |
| Effect | Therefore, when a car rounds a bend the friction between its tyres and the road provides a net centripetal force (external force) which allows the car to undergo circular motion, hence rounding the bend. However, when the road is icy there is little to no friction between the tyres and the road. |
| Outcome | Hence, no external force is exerted on the car and by Newton’s First Law, the car continues to travel straight ahead at its original velocity and fails to turn the corner. |
Thus, our logical and sequential answer is below:
Newton’s first law states that an object will continue in its state of motion unless acted upon by an external force. Therefore, when a car rounds a bend the friction between its tyres and the road provides a net centripetal force (external force) which allows the car to undergo circular motion, hence rounding the bend. However, when the road is icy there is little to no friction between the tyres and the road. Hence, no external force is exerted on the car and by Newton’s First Law, the car continues to travel straight ahead at its original velocity and fails to turn the corner.
Question 3 solution
Part (a)
Rearranging v = u + at yields:
\begin{aligned} a &= \dfrac{v - u}{t} \\ &= \dfrac{15}{7.5} \\ &= 2 \ ms^{-2} \end{aligned}
Answer: 2 \ ms^{-2}
Part (b)
From Newton’s Second Law:
\begin{aligned} F_{net}& = m\vec{a} \\ &= (540)(2) \\ &= 1080 \ N \end{aligned}
Answer: 1080 \ N
Part (c)
By drawing a diagram of the car and the forces acting on it, we are able to see how the forces interact with each other:

Hence, the net force on the car can be found by evaluating the horizontal forces acting on it:
\begin{aligned} F_{net} &= driving \ force - frictional \ force \\ &= 1600 - f \\ \therefore f&=1600 - F_{net} \end{aligned}
From part(b), we now that the net force on the car is 1080 \ N . Substituting yields:
f = 1600 - 1080 = 520 \ N
Answer: 520 \ N
Question 4 solution
Part (a)
The diagram drawn must display the Normal Reaction Force, the Weight Force and the Frictional Force:
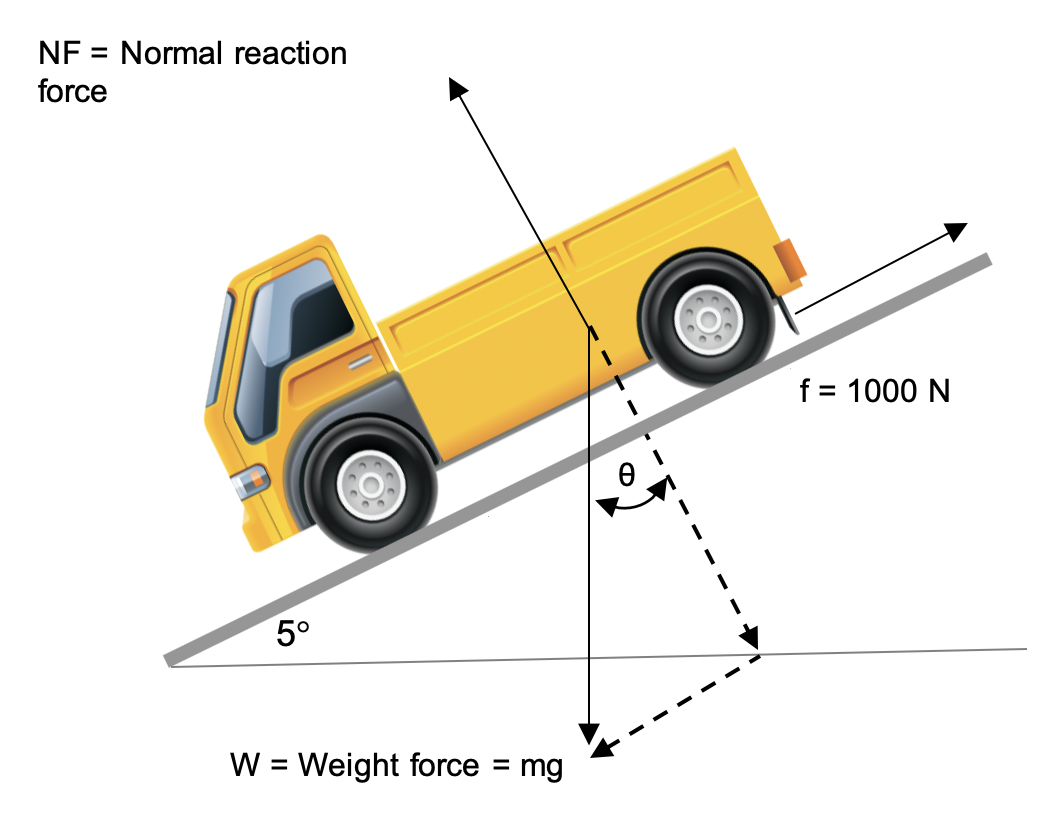
Part (b)
The net force acting along the slope must be zero if the downhill velocity remains constant.
Answer: 0
Part (c)
As the car is moving at a constant velocity, the resistive forces acting up the hill must balance the downhill component of weight force:
\begin{aligned} mg sin \theta &= 1000 \ N \\\\ m &= \frac{1000}{g sin \theta} \\\\ m &= \frac{1000}{9.8 sin 5 \degree} \\\\ \therefore m &= 1171 \ kg \ (4 \ s.f.) \end{aligned}
Answer: 1171 \ kg
Question 5
Part (a)
Step 1: Draw a free body diagram of each object (including internal forces) to find the expression of net force on each object.
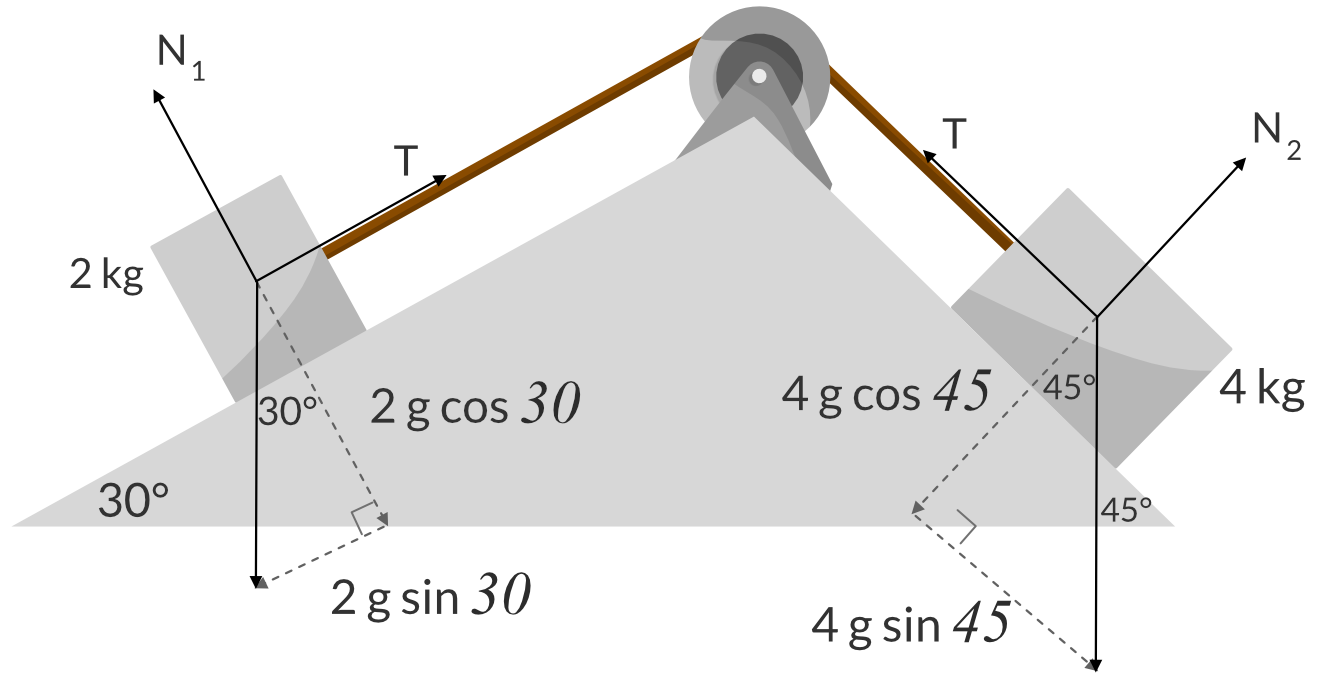
Step 2: Find the net external force on the entire system and apply Newton’s second law to find the acceleration.
The external forces acting on the blocks are:
- The component of the weight of block 1 resting on the slope \theta = 30 \degree : 2gsin30\degree
- The component of the weight of block 2 resting on the slope \theta = 45 \degree : 4gsin45\degree
We can ‘unfold’ this problem to make it look like blocks connected by string.
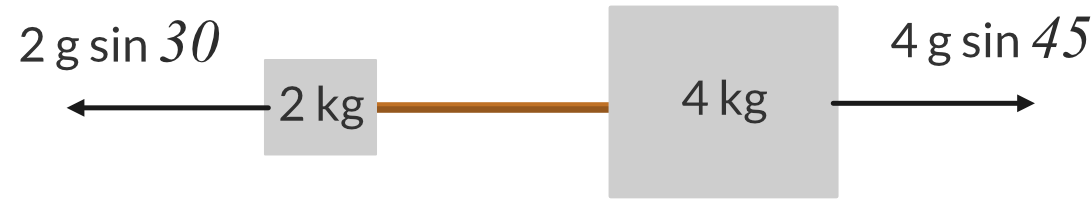
Hence, the acceleration of the blocks is given by:
\begin{aligned} a &= \frac{F_{net}}{m_{total}} \\ &= \frac{4g sin 45\degree - 2g sin 30 \degree}{4 + 2} \\ &= 2.986... \\ &= 3.0 \ ms^{-2} \ (2 \ s.f.) \end{aligned}
Answer: 3.0 \ ms^{-2}
Part (b)
Step 1: Add the forces acting on the 2kg block
\begin{aligned} \Sigma F &= ma \\ T - 2gsin30\degree &= 2a \\ T = 2gsin30\degree &+ 2a \end{aligned}
Step 2: Substitute the value of acceleration into the tension equation to find the value of T.
\begin{aligned} T &= 2gsin30\degree + 2a \\ &= 2 \times 9.8 sin 30\degree + 2 \times 3.0 \\ &= 15.7728... \\ &= 15.8 \ N \ (3 \ s.f.) \end{aligned}
Answer: 19.9 \ N
Question 6 solution
Part (a) To plot a graph of maximum static friction vs mass, we need to find the average applied force that causes the mass to slip.
Step 1: Determine the maximum static friction (f_{s(max)} ) , per mass, for each surface combination.
| Mass (kg) | Average Applied Force (N) | f_{s(max)} |
| 0.25 | 1.9 | 1.9 |
| 0.35 | 2.9 | 2.9 |
| 0.45 | 3.7 | 3.7 |
| 0.55 | 4.7 | 4.7 |
| 0.65 | 5.2 | 5.2 |
Step 2: Graph the results derived in Step 1, showing the relationship between f_{s(max)} and the independent variable. Draw a line of best fit on the graph.
A graph of f_{s(max)} vs mass (m) for the sandpaper-wood surface is shown below:
Part (b): To determine the significance of the gradient, rearrange the equation f_{s(max)}= \mu_s mg in the form y = mx.
Given
- f_{s(max)} = \mu_s N =\mu_s mg
- f_{s(max)}= \mu_s mg
- \therefore f_{s(max)} =(\mu_sg) \times m
The graph of f_{s(max)} vs mass (m) is linear.
- f_{s(max)} is the dependent variable (y-axis)
- m is the independent variable (x-axis)
- \therefore gradient =(\mu_sg)
Part (c)
Step 1: Calculate the gradient of the line of best fit.
\begin{aligned} gradient &= \frac{rise}{run} \\ &= \frac{4.6 - 2.2}{0.56 - 0.28} \\ &= 8.6 \end{aligned}
Step 2: Using the results obtained in (b), calculate the coefficient of static friction.
We can derive a relationship between the coefficient of static friction and the gradient of the line of best fit:
\begin{aligned} \therefore gradient &= \mu_s g \\ \therefore \mu_s &= \frac{gradient}{g} \\ &= \frac{gradient}{9.8} \\ &= \dfrac{8.6}{9.8} \\ &= 0.88\end{aligned}
Answer: 0.88
Question 7 solution
Part (a)
Before we use the formula to calculate work done, we must find the component of force in the direction of displacement F_x . This is because force in the y-direction does not impact the horizontal movement of the tyre.
\begin{aligned} W &= F_xd \\ &= (250 cos 20\degree)(25) \\ &= 5873.07... \ J \end{aligned}
Answer: 5900 \ J (2 s.f.)
Part (b)
Step 1: Calculate the work required to overcome the frictional force.
To move the tyre from its position at rest, work must be done to overcome the frictional force between the tyre and the ground. The amount of work required to overcome this frictional force is given by:
\begin{aligned} W_f &= F_fd \\ &= (220)(25) \\ &= 5500 \ J \end{aligned}
Step 2: Calculate the kinetic energy Floyd provides the tyre.
Therefore, the component of work done by Floyd in providing the tire kinetic energy is equivalent to:
\begin{aligned} W_{KE}& = W_{Simon} - W_f \\ &= 5873 - 5500 \\ &= 373 \ J \end{aligned}
Step 3: Calculate the tyre’s velocity by rearranging the formula for kinetic energy.
This means the tyre possess 373 \ J of kinetic energy as a result of the work done by Floyd. Hence, the tyre’s velocity is given by:
\begin{aligned} v&= \sqrt{2KE}{m} \\ &= \frac{2(373)}{60} \\ &= 3.5260... \ ms^{-1} \end{aligned}
Answer: 3.5 \ ms^{-1} (2 s.f.)
Question 8 solution
The change in momentum and thus impulse is fixed.
I = \vec{F} \Delta t , so \vec{F} = \dfrac{I}{ \Delta t} , which is an inverse relationship.
The only graph showing an inverse relationship is graph C.
Answer: (C)
Question 9 solution
Part (a): By the Law of Conservation of Energy, the total energy of the ball is fixed:
KE_{initial} + PE_{initial} = KE_{final} + PE_{final}
Step 1: Calculate the ball’s initial kinetic energy.
The ball starts off with a kinetic energy of KE_{initial} = \bigg( \frac12 \bigg) (0.5)(2^2) = 1 \ J
Step 2: Calculate the ball’s final kinetic energy.
When it reaches the ground, all of the ball’s potential energy has been converted to kinetic energy, therefore PE_{final} = 0 .
Hence:
\begin{aligned} KE_{final} &= KE_{initial} + PE_{initial} \\ &= 1 + mgh \\ &= 1 + (0.5)(9.8)(10) \\ &= 50 \ J \end{aligned}
Step 3: Find an expression for momentum in terms of kinetic energy and mass only.
From the formula for kinetic energy, v = \sqrt{ \dfrac{2KE}{m}} .
We can substitute this into the formula for momentum p = mv to obtain a new expression in terms of KE and m:
\begin{aligned} p &= mv \\ &= m \sqrt{\dfrac{2KE}{m}} \\ &= \sqrt{2mKE} \end{aligned}
Step 4: Substitute the calculated values into this equation to calculate the ball’s momentum.
Substituting the calculated value for KE_{final} yields:
\begin{aligned} p &= \sqrt{2mKE} \\ &= \sqrt{ 2 \times 0.50 \times 50} \\ &= 7.071... \\ &= 7.07 \ kgms^{-1} \ (3 \ s.f.) \end{aligned}
Answer: 7.07 \ kgms^{-1}
Part (b)
Step 1: Rearrange the first equation of motion to obtain an expression relating time and acceleration.
Rearranging the first equation of motion, we obtain an expression relating the known variables time (t) and acceleration (a) :
\begin{aligned} v &= u + at \\ v-u &= at \\ &= 6 \times 3 \\ \therefore v - u &= 18 \end{aligned}
Step 2: Use this expression to calculate the impulse.
We can now use this difference in velocities to find the change in momentum of the mass:
\begin{aligned} \Delta p &= m(v-u) \\ &= 5(18) \\ &= 90 \ kgms^{-1} \end{aligned}
Answer: 90 \ kgms^{-1}
Question 10 solution
Part (a)
\begin{aligned} p &= mv \\ &= 1500 \times 16 \\ &= 24000 \ kgms^{-1} \ East \end{aligned}
Answer: 24000 \ kgms^{-1} \ East
Part (b)
\begin{aligned} p &= mv \\ &= 2500 \times 20 \\ &= 50000 \ kgms^{-1} \ North \end{aligned}
Answer: 50000 \ kgms^{-1} \ North
Part (c)
Step 1: Calculate the initial momentum of the car and the truck together. Be sure to indicate the direction.
To calculate the initial momentum of the car and truck together, we can draw a vector triangle.
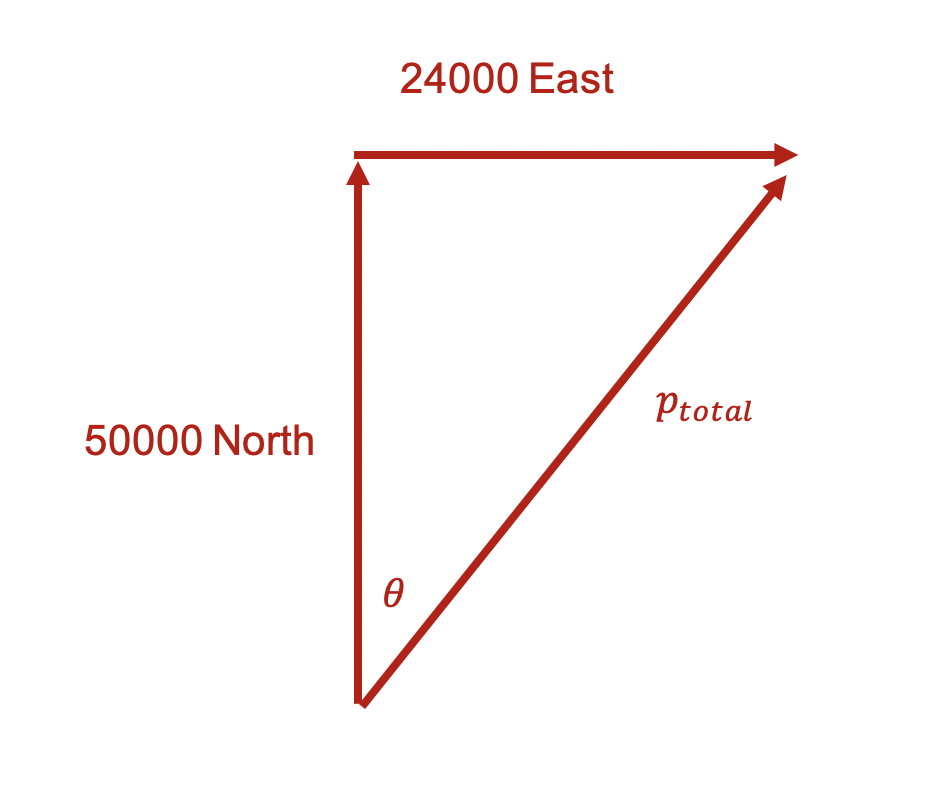
As the vector triangle is right-angled, we can use trigonometry to calculate the magnitude and direction of their initial momentum p_{total} .
\begin{aligned} p_{total} &= \sqrt{24000^2 + 50000^2} \\ &= 55461.69... \\ &= 55462 \ kgms^{-1} \\ \theta &= tan^{-1} \bigg( \frac{2.4}{5} \bigg) \\ &= 25.64... \\ &= 25.6 \degree \\ \therefore p_{initial} &= 55462 \ kgms^{-1} \ N25.6\degree E \end{aligned}
Step 2: Use the value for initial momentum calculated in step 1 to calculate the final velocity of the car and the truck together.
The Law of conservation of momentum states that “the sum of momenta before a collision is equal to the sum of momenta after a collision”. Hence, the initial momentum is equal to the final momentum. Using this, we can calculate the final velocity of the car and the truck:
\begin{aligned} v&= \frac{p}{m} \\ &= \frac{55462}{4000}\\ &= 13.8655 \\ & = 13.9 \ ms^{-1} \ N25.6 \degree E \end{aligned}
Answer: 13.9 \ ms^{-1} N25.6 \degree E
Need more practice questions on Module 2 Dynamics?
Test your depth of understanding of Module 2 ‘Dynamics’ in just 10 minutes with Learnable’s customisable quiz builder. There are over 500+ exam-style questions for each module. Instant feedback provides immediate adjustments on your misconceptions. Try Learnable for free now.
Learnable Education and www.learnable.education, 2019. Unauthorised use and/or duplications of this material without express and written permission from this site's author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Learnable Education and www.learnable.education with appropriate and specific direction to the original content.